Question

Explain with the help of a labeled diagram the distribution of the magnetic field due to a current through a circular loop. Why is it that if a current-carrying coil has $N$ turns, the field produced at any point is n times as large as that produced by a single turn?

Answer 1

To answer this question, we have to first draw a diagram for a current through a loop. To answer the second part, we should remember the formulae of the magnetic field Biot Savart’s law for the magnetic field produced by a circular loop. We can write the magnetic field for one loop and then the magnetic field for $N$ turns and compare.

Formulae used:
$B = \dfrac{{{\mu _0}NI}}{{4\pi R}}$
Here $B$ is the magnetic field produced due to a circular loop, $N$ is the number of turns, $I$ is the current carried by the loop, ${\mu _0}$ is the permeability of free space and $R$ is the radius of the loop.

Complete answer:

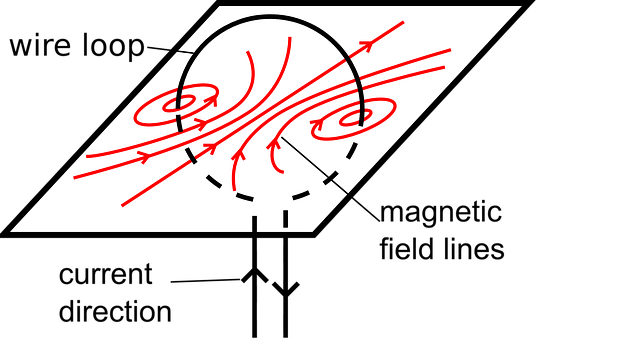
In the above figure, $B$ is the magnetic field that has magnetic field lines produced due to a circular loop and $I$ is the current carried by the loop and its direction in the loop. we can clearly see that using the right-hand thumb rule we can easily predict the direction of magnetic field lines.
In figure $(a)$ , we are trying to find the direction using the right-hand rule, where the thumb points toward the direction of current flow and the curling of fingers show the direction of the magnetic field.
In figure $(b)$ , shows the direction of the magnetic field.
We know that
$\Rightarrow B = \dfrac{{{\mu _0}NI}}{{4\pi R}}$
Here $B$ is the magnetic field produced due to a circular loop, $N$ is the number of turns, $I$ is the current carried by the loop, ${\mu _0}$ is the permeability of free space and $R$ is the radius of the loop.
For one turn the amount current flowing in the loop will be $I$
So the magnetic field will be
$\Rightarrow {B_1} = \dfrac{{{\mu _0}I}}{{4\pi R}}$
But for $N$ turns, the current will also increase $N$ times. So the magnetic field will be,
$\Rightarrow {B_N} = \dfrac{{{\mu _0}NI}}{{4\pi R}} = N{B_1}$
So we know that the magnetic field of a current-carrying loop increases with an increase in the number of turns of the loop.

Note: While calculating the magnetic field for the object, make sure to use the correct formulae. For example, here we need to use the formula for the magnetic field for a loop. So no need to use the formulae of the magnetic field for a wire. Also while finding the direction of the magnetic field for any current-carrying wire or loop, make sure to use the right-hand rule correctly.