Question

Explain with suitable diagrams and appropriate examples why some non-ideal solutions show positive deviation from ideal behavior.

Answer 1

We can explain the deviation by looking at the inter-molecular interactions among solute-solvent particles in a non-ideal solution.

Complete Answer
When molecules of a substance in liquid phase escape to vapor phase, it gives rise to vapor pressure. Generally, we use the term volatility for this escaping tendency. So, a highly volatile liquid will have a high vapor pressure. However, it has been established that there is a force of attraction between the particles in a substance, then how can they escape? Well, the simple answer would be that the intermolecular forces would be overcome, bonds would be broken and the molecules would escape. This is exactly what we help them with by increasing temperature.
Here, we will see what will happen to the molecules or the vapor pressure of a volatile liquid when it will form a solution with another liquid. Let’s represent the liquids as $X\;and\;Y$ in which the initial interactions are $\left( {X - X} \right){\rm{ and }}\left( {Y - Y} \right)$. Now that a solution has been formed, molecules of the two liquids would also interact with each other and we will also have $\left( {X - Y} \right)$ interactions.
Depending on the nature of these intermolecular interactions, we can classify the liquid-liquid solutions as:
- Ideal solutions: In these solutions, the interactions $\left( {X - X} \right){\rm{ and }}\left( {Y - Y} \right)$ are almost equal to $\left( {X - Y} \right)$ interactions. For example: Solution of $n - hexane\;and\;n - heptane$ and that of benzene and toluene
- Non-ideal solutions: In these solutions, the interactions $\left( {X - X} \right){\rm{ and }}\left( {Y - Y} \right)$ are not equal to $\left( {X - Y} \right)$ interactions but can be weaker or stronger.
For ideal solutions, we have Raoult’s law that can be expressed mathematically as follows:
${p_{\rm{X}}} = p_{\rm{X}}^0{\chi _{\rm{X}}}$
Here, ${p_{\rm{X}}}$is the vapor pressure of the component ${\rm{X}}$ in the solution, $p_{\rm{X}}^0$ is the vapor pressure of ${\rm{X}}$as a pure solvent at the same temperature and ${\chi _{\rm{X}}}$ is the mole fraction of ${\rm{X}}$ in the solution.
So basically, we have a linear relationship between the vapor pressure of a component and its mole fraction in its ideal solution. However, in non-ideal solutions, there is a deviation from linearity. It can be of two types:
1. Positive deviations:** In these solutions, the interactions $\left( {X - X} \right){\rm{ and }}\left( {Y - Y} \right)$ are stronger than the $\left( {X - Y} \right)$ interactions. It means that upon mixing, the intermolecular forces are weaker and thus it becomes easier to escape giving a higher vapor pressure than expected.
2. Negative deviations: In these solutions, the interactions $\left( {X - X} \right){\rm{ and }}\left( {Y - Y} \right)$ are weaker than the $\left( {X - Y} \right)$ interactions. It means that upon mixing, the intermolecular forces are stronger and thus it becomes more difficult to escape giving a lower vapor pressure than expected.
We can represent these diagrammatically as follows:

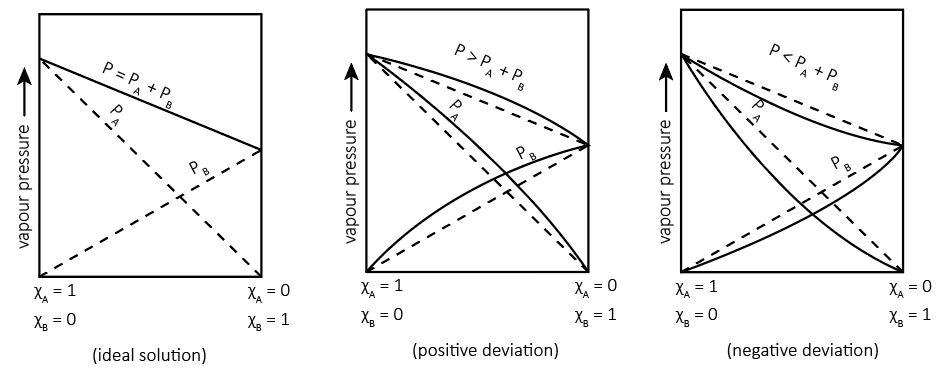
As it is evident that the ideal solutions follow Raoult’s law and we can see the linear relationship whereas non-ideal solutions are deviated and don’t follow Raoult's law.
Let’s take an example of a non-ideal solution that shows positive deviation: solution of ${C_2}{H_5}OH$ and $C{H_3}\left( {CO} \right)C{H_3}$. In the pure ethanol, we have hydrogen bonding known for its strength, between the ethanol molecules for the presence of hydroxyl group:

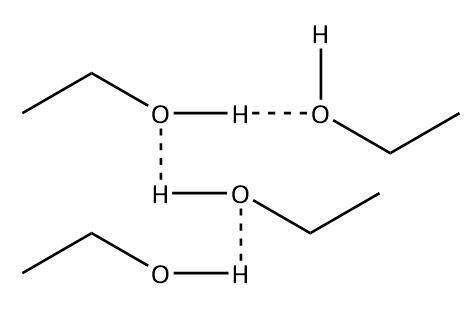
However, no such hydrogen bonding is present between the ethanol-acetone molecules in the solution. This weakening of intermolecular forces results in positive deviation.
Note:
We have to keep in mind that classification of deviation is based on Raoult’s law but reason originates from the intermolecular interactions.