Question

Explain with a suitable diagram and appropriate examples why some non-ideal solutions show positive deviation from ideal behaviour.

Answer 1

Non -ideal solutions doesn’t satisfy the Raoult’s condition i.e. ${{\text{p}}_{A}}\ne \text{p}_{A}^{\circ }{{\text{x}}_{A}}$ and ${{\text{p}}_{B}}\ne \text{p}_{B}^{\circ }{{\text{x}}_{B}}$ but such solutions shows positive deviation when ${{\text{p}}_{A}}\text{p}_{A}^{\circ }{{\text{x}}_{A}}$ and ${{\text{p}}_{B}}\text{ p}_{B}^{\circ }{{\text{x}}_{B}}$ and when the total vapour vapour is always greater than the individual vapour pressure i.e. p=${{\text{p}}_{A}}\text{+}{{\text{p}}_{B}}$ is always greater than the $\text{p}_{A}^{\circ }{{\text{x}}_{A}}$+$\text{ p}_{B}^{\circ }{{\text{x}}_{B}}$.

Complete Solution :
First of all, what are non-ideal solutions? The solution which doesn’t obey Raoult's law over the entire range of temperature are called the non-ideal solutions. Raoult’s law states that at a given temperature, for a solution of volatile liquids, the partial vapour pressure of each component in solution is equal to the product of the vapour pressure of the pure component and its mole fraction. Therefore, for such solutions:
${{\text{p}} _{A}} \ne \text{p}_{A}^{\circ }{{\text{x}}_{A}}$ and ${{\text{p}}_{B}}\ne \text{p}_{B}^{\circ }{{\text{x}}_{B}}$
Here, ${{\text{p}}_{A}}$ and ${{\text{p}}_{B}}\text{ }$ are the vapour pressure of the solvents A and B , $\text{p}_{A}^{\circ }$ and $\text{p}_{B}^{\circ }$ are the vapour pressures of the pure component and ${{\text{x}}_{A}}$ and ${{\text{x}}_{B}}$ are the mole fractions of the components A and B.

- There are certain non- ideal solutions which show positive deviation from ideal behaviour. Consider a binary solution of two components A and B. If the A-Interactions in the solutions are weaker than the A-A and B-B interactions in two liquids forming the solution, then the escaping tendency of both the A and B types of molecules from the solution becomes more than from pure liquids. As a result, each component of solution has a partial vapour pressure greater than expected on the basis of Raoult’s law. The total vapor pressure will be greater than corresponding vapour pressure expected in case of ideal solution of the same composition and this type of behaviour of solution is known as positive deviations from Raoult’s law.
Mathematically, it may be expressed as:
${{\text{p}} _{A}} \text{p}_{A}^ {\circ} {{\text{x}} _{A}}$ and ${{\text{p}} _{B}} \text{p}_{B}^ {\circ} {{\text{x}} _{B}}$

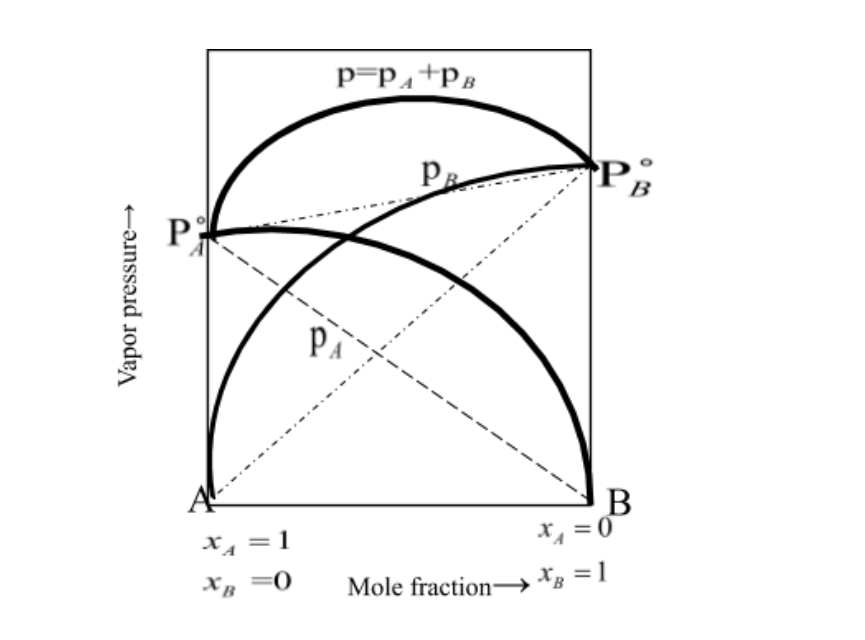
Here, dotted lines show the ideal behaviour upon mixing while the thick lines indicate the actual behaviour.
The total vapour pressure:
p=${{\text{p}}_{A}}\text{+}{{\text{p}}_{B}}$ is always greater than the $\text{p}_{A}^{\circ }{{\text{x}}_{A}}$+$\text{ p}_{B}^{\circ }{{\text{x}}_{B}}$
Examples of such non-ideal solutions which show positive deviation from Raoult’s law are: ethyl alcohol and cyclohexane, acetone and carbon disulphide etc.

Note: Non-ideal solutions are generally accompanied by the changes in the enthalpy and volume during their formation as they don’t obey the Raoult’s law i.e.
${{\Delta} _{mixing}} \text{H}\ne \text {0}$ and ${{\Delta} _{mixing}} \text{V}\ne \text {0}$