Question

Explain the term Fresnel distance.

Answer 1

In order to answer the above question, we will discuss the concept of diffraction in optics. We will be discussing the Fresnel diffraction through a single slit and finally, we will understand the term Fresnel distance.

Complete step by step solution:
As we all know, light moves through a medium. In a medium, light moves as an electromagnetic wave.
If something gets in the way of the light, it bends slightly and changes its course. After light is deflected, the width of the incoming light changes. The principle of diffraction explains this deflection. The definition of Fresnel's distance describes the correlation of the width of light waves before and after deflection.
First of all, lets understand the diffraction of light.

The subtle bending of light as it moves around the edge of an object is known as diffraction. The amount of bending is determined by the wavelength of light's size in relation to the opening's size.
Secondly, let’s discuss Fresnel distance.
By comparing the width of a slit to the spread caused by light diffraction, Fresnel developed a theory. Consider a slit with a width of $a$ and a distance of screen from the slit of $z$.

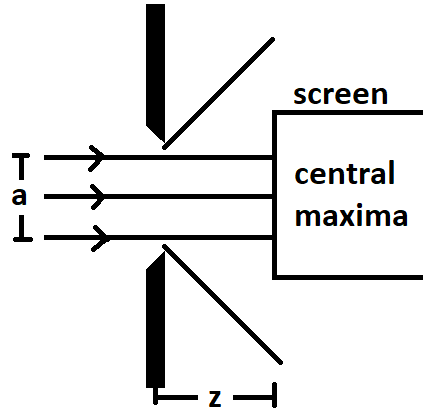
The angular width of the central maxima obtained on the screen, $\theta$ will be given by
$\theta =\dfrac{\lambda }{a}$
Where $\lambda$ is the wavelength and $a$ is the slit width.
The spread of the diffracted light on the central maxima, $y$ and the distance of the screen from slit can be represented as,

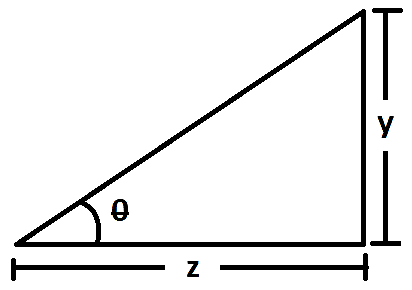
The spread of the diffracted light on the screen is provided by,
$\tan \theta \approx \theta =\dfrac{y}{z}$
Since, $\theta =\dfrac{\lambda }{a}$
$\begin{aligned} & \Rightarrow \dfrac{\lambda }{a}=\dfrac{y}{z} \\\ & \therefore y=\dfrac{z\lambda }{a} \\\ \end{aligned}$
So the spread of the central maxima on the screen will be $\dfrac{z\lambda }{a}$.
Let’s discuss a limiting condition for the spreading of central maxima,
If spread of central maxima = slit width
$\begin{aligned} & y=a \\\ & \Rightarrow a=\dfrac{z\lambda }{a} \\\ \end{aligned}$
But the spread of central maxima cannot be equal to the slit width for all values of $z$. There will be some specific values of $z$for this condition.
Let us assume distance travelled by ray, $z$becomes ${{z}^{f}}$for $y=a$
So Fresnel distance describes the distance at which spread due to diffraction becomes comparable to the width of the slit or not.
$\Rightarrow {{z}^{f}}=\dfrac{{{a}^{2}}}{\lambda }$
If the values of $z$are less than the ${{z}^{f}}$then the spreading of central maxima will be approximately equal to the slit width, $a$.
The limiting conditions for spreading of central maxima are provided as,

& z<{{z}^{f}} \Rightarrow y \text{<}a \\\ & z={{z}^{f}}\Rightarrow y\approx a \\\ & z>{{z}^{f}}\Rightarrow y \text{>}a \\\ \end{aligned}$$ So, the distance of the screen from the slit, such that the spreading of light due to diffraction from the center of the screen is just equal to the size of the slit is called Fresnel distance. **Note:** It is very important to note here that the Fresnel distance is usually a dimensionless quantity. This formula plays an important role in the existence of ray optics. Until and unless the Fresnel distance is equal to the slit width, Ray optics is used. Whereas, if the Fresnel distance becomes greater than the slit width, then the wave optics comes into play.