Question

Explain the parallax method for measuring large distances. With the help of it, explain the method to determine the shape of a heavenly body.

Answer 1

This question is purely based on the understanding of the topic, so the parallax method should be properly clear for solving this question. In this question, take all the cases in consideration before reaching a solution and we can make a diagram for reference purpose, so that the points can be explained properly.

Complete solution:
Measurement of Large Distances :-
Length: It is defined as the difference between two positions taken by two events that occur instantly.
Parallax Method: When an object is seen by closing our right and left eye alternatively, there is a shift in the position of the object w.r.t. the background observed. This is known as parallax.
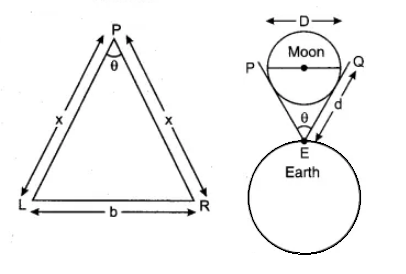
Imagine an object $P$ placed at a distance $x$ from our eyes. Let the line joining the object to the left and right eye make $O$ angle w.r.t. each other. $O$ is called parallax angle.
The distance $LR$ is called basis. ​
$\begin{aligned} & \theta =\dfrac{Length\,of\,Arc}{Radius} \\\ & \Rightarrow \theta =\dfrac{b}{x} \\\ & \therefore x=\dfrac{b}{\theta } \\\ \end{aligned}$
Size of Astronomical Object: Diameter of Moon: Let Moon be the astronomical object whose diameter is to be measured. We observed the Moon with the help of a telescope. Let it be observed from a place $F$ on Earth and make an angle $O$ with the two ends $P$ and $Q$ of moon and the point $K$, as shown in fig. 1.5. 0 is called the angular diameter of the Moon.
Let $d$ be the distance of the Moon from the Earth.
Then, angular diameter,
$\begin{aligned} & \theta =\dfrac{\overline{PQ}}{d}=\dfrac{Length\,of\,Arc}{Radius} \\\ & \Rightarrow \,\theta =\dfrac{D}{d} \\\ & \therefore D=\theta d \\\ \end{aligned}$​​
Reflection or Echo Method: A gun is fired towards the hill and the time taken between instant of firing and hearing of echo bet. In this time interval, sound first travels towards the hill from the place of firing and then hack from the hill to the place of firing. Let $u$ be the speed of sound. $x$ be the distance of hill from the place of firing the gun, then,
$\begin{aligned} & 2x=v\times t \\\ & \therefore \,x=\dfrac{vt}{2} \\\ \end{aligned}$

Note:
The main thing in this question is to understand the parallax method and to take all the cases into consideration for calculating the measurement of large distances. And explaining the cases using an example simplifies the solution and also gives a clear understanding of the solution, which helps to understand the cases that you have stated.