Question

Explain series combination of capacitors. Derive the formula for equivalent capacitance.

Answer 1

Several capacitors for a range of applications may be paired together. As a single equal condenser, several capacitor links work. Both the individual capacitors and how they are related depend on the overall capability of this equivalent one capacitor.

Complete solution:
Capacitors can be arranged as series and parallel in two simple and common relation forms for which the overall capacitance can be easily measured. The series and parallel of these two simple variations can be used even as part of complex relations. The reciprocal number of the equivalent capacitance is the sum of the reciprocal capacities of each capacitor in a series combination.

As for every capacitor, it relies on load and voltage by means of the capacitance of the mixture. Each capacitor acquires the same charge Q when the series combination is attached to a battery with voltage V. Firstly, the battery's positive terminal charge is $+ Q$ and the negative terminal charge is $- Q$. To illustrate, it cannot be skipped on the plate. Charges on the other plates are then caused to zero on all plates except for every pair of capacitor plates. The number of charges is 0. The potential drop ${V_1} = \dfrac{Q}{{{C_1}}}$ on one capacitor could be different, as the capacitor normally has different capacities, from the potential drop ${V_2} = \dfrac{Q}{{{C_2}}}$ on another condenser. The two or three-condenser combination series looks like a single capacitor with less power.

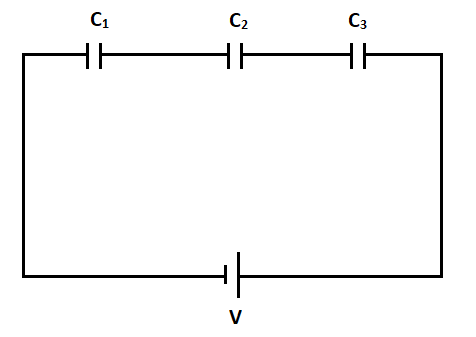
Now, as given in the figure, consider three capacitors ${C_1}, {C_2}$ and ${C_3}$ are connected in series combination,
Now, the charge on first capacitor would be, ${Q_1} = {C_1} {V_1}$
The charge on second capacitor would be, ${Q_2} = {C_2} {V_2}$
The charge on third capacitor would be, ${Q_3} = {C_3} {V_3}$
In series combination, all the charges are equal, or,
${Q_1} = {Q_2} = {Q_3} = Q$
Also, the total voltage will be,
$V = {V_1} + {V_2} + {V_3}$
Therefore,
$Q = {C_ {Eq}} V$
on writing above equation in terms of voltage, we have
$V = \dfrac{Q}{{{C_{Eq}}}}$
$\dfrac{{Q}}{{{C_{eq}}}} = \dfrac{{Q}}{{{C_1}}} + \dfrac{Q}{{{C_2}}} + \dfrac{Q}{{{C_3}}}$
Now, on further solving, we get
$\Rightarrow \dfrac{{1}}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$

The expression for equivalent capacitance in series combination is $\dfrac{{1}}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$.

Note: The series combination of two or three capacitors resembles a single capacitor with a lower capacitance. Remember that the total capacitance of the capacitors coupled in series is equal to their equivalent capacitance and also smaller than the smallest of the capacitances in that series combination.