Solveeit Logo
Login

Question

Question: Explain positive, negative and zero work. Give one example of each....

Explain positive, negative and zero work. Give one example of each.

Explanation

Solution

Hint: Write formula of work W=F→⋅r→W=\overrightarrow{F}\cdot \overrightarrow{r}. Learn dot product of two forces. For positive work, W should be positive so for this find an angle between force and displacement.
Dot product of two component A and B
A→⋅B→=ABcos⁡θ\overrightarrow{A}\cdot \overrightarrow{B}=AB\cos \theta
Where θ\theta is the angle between two vectors.
F→⋅r→=Frcos⁡θ\overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta
Find θ\theta for positive W, negative W and zero W.

Complete step by step answer:
The work done by a force on a particle during a displacement is given as
W=F→⋅r→W=\overrightarrow{F}\cdot \overrightarrow{r}
Here, W = work
F→\overrightarrow{F}= force
r→\overrightarrow{r}= displacement
Positive work done – The work done is said to be positive when force and displacement are in the same direction.
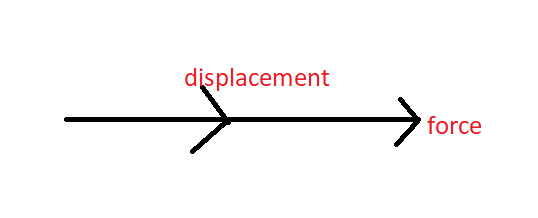
θ=0∘ F→⋅r→=Frcos⁡θ F→⋅r→=Frcos⁡0∘ F→⋅r→=Fr W=F→⋅r→=Fr \begin{aligned} & \theta ={{0}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{0}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr \\\ & W=\overrightarrow{F}\cdot \overrightarrow{r}=Fr \\\ \end{aligned}

Hence, work is positive.

Zero work – the work done is said to be zero when force and displacement are perpendicular to each other.
θ=90∘ F→⋅r→=Frcos⁡θ F→⋅r→=Frcos⁡90∘ F→⋅r→=0 W=F→⋅r→=0 \begin{aligned} & \theta ={{90}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{90}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=0 \\\ & W=\overrightarrow{F}\cdot \overrightarrow{r}=0 \\\ \end{aligned}
Hence, work is zero

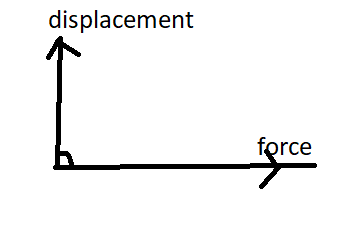
Negative work done – The work done is said to be negative when force and displacement are in opposite directions.

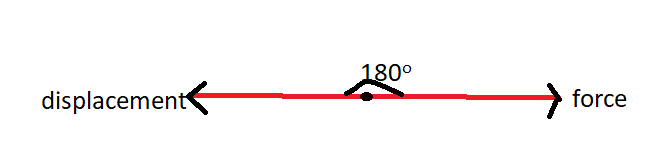
θ=180∘ F→⋅r→=Frcos⁡θ F→⋅r→=Frcos⁡180∘ F→⋅r→=−Fr W=F→⋅r→=−Fr \begin{aligned} & \theta ={{180}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{180}^{{}^\circ }} \\\ & \overrightarrow{F}\cdot \overrightarrow{r}=-Fr \\\ & W=\overrightarrow{F}\cdot \overrightarrow{r}=-Fr \\\ \end{aligned}
Hence, work is negative.

Note: Work done by friction is always zero because friction force and displacement act in opposite directions. When a spring travels from A to B and from B back to A then work done during the return journey is negative of the work during the onwards journey and the net work done by the spring is zero.