Question

Find the equations of tangents and normals to the curve at the point on it.

$y = x^2 + 2e^x + 2$ at (0, 4)

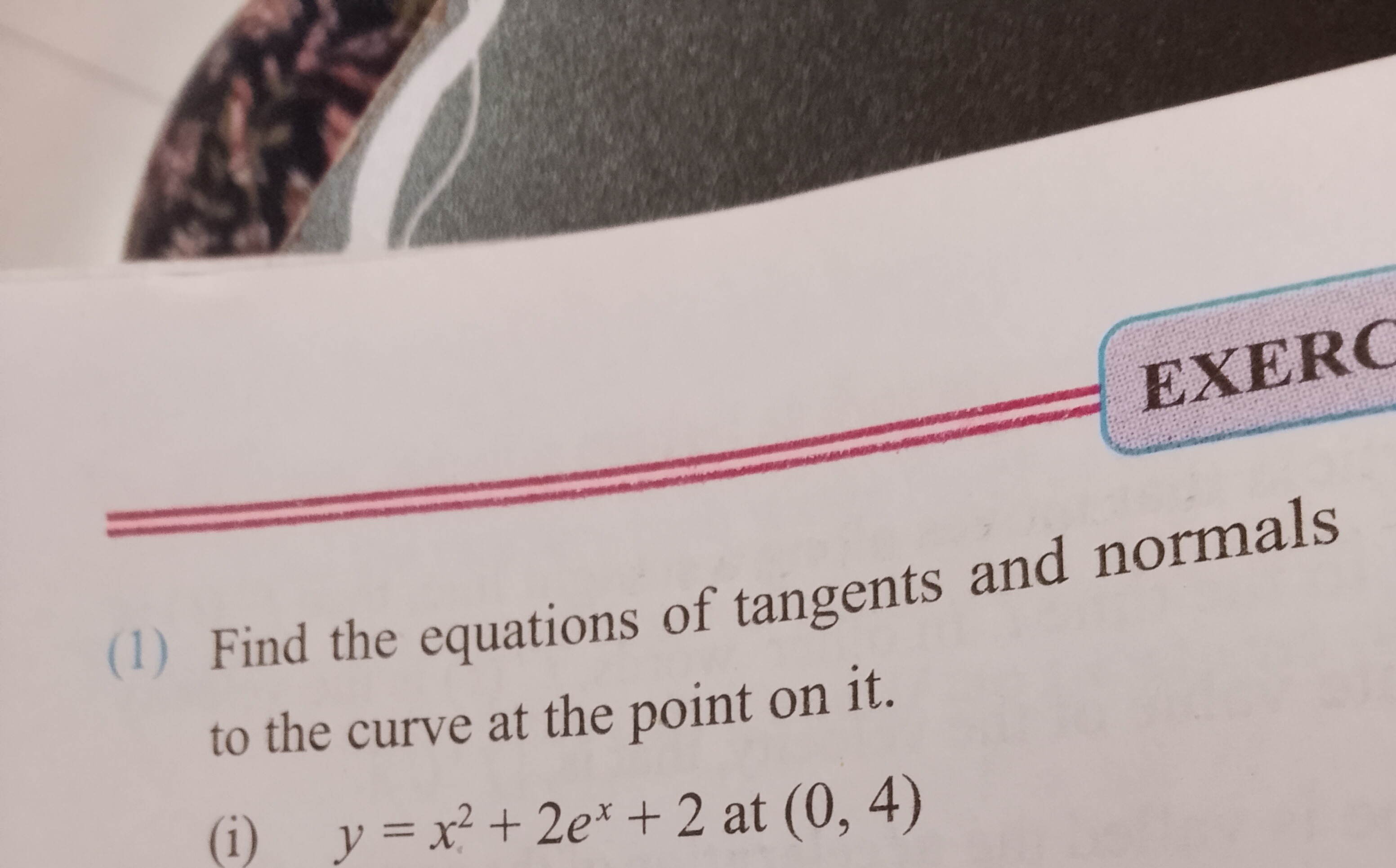
Answer 1

Tangent: $\displaystyle y = 2x + 4$

Normal: $\displaystyle y = -\frac{x}{2} + 4$

Answer 2

1. Given the curve

   $$y = x^2 + 2e^x + 2$$

   Differentiate with respect to $x$:

   $$\frac{dy}{dx} = 2x + 2e^x.$$

2. At the point $(0, 4)$:

   $$\left.\frac{dy}{dx}\right|_{x=0} = 2(0) + 2e^0 = 2.$$

   So, the slope of the tangent is 2.

3. Equation of the tangent line (using point-slope form):

   $$y - 4 = 2(x - 0) \quad \Rightarrow \quad y = 2x + 4.$$

4. The slope of the normal is the negative reciprocal of 2, i.e.,

   $$m_{\text{normal}} = -\frac{1}{2}.$$

5. Equation of the normal line:

   $$y - 4 = -\frac{1}{2}(x - 0) \quad \Rightarrow \quad y = -\frac{x}{2} + 4.$$

Explanation (Core Steps):

• Differentiate $y = x^2 + 2e^x + 2$ to get $\frac{dy}{dx} = 2x + 2e^x$.
• At $x=0$, slope $=2$.
• Tangent: $y = 2x + 4$.
• Normal: Slope $-\frac{1}{2}$, Equation: $y = -\frac{x}{2} + 4$.