Question

Excluding stoppages, the speed of a bus is 72 kmph ,and including stoppages, is 60 kmph. For how many minutes does the bus stop per hour?
a. 12
b. 8
c. 15
d. 10

Answer 1

Hint: Think of the basic definition of speed and focus on the point that the speed mentioned here is the average speed.
Let’s start with what is speed. Speed is a scalar quantity defined as the distance travelled by a particle or object per unit time.

Complete step-by-step answer:
Generally, we deal with two kinds of speeds. One is instantaneous, and the other is the average speed. For uniform motion, both are identical.

Average speed is defined as the total distance covered by a body divided by the time taken by the body to cover it.
$\therefore {{v}_{avg}}=\dfrac{\text{distance covered}}{\text{time taken}}$

Now, starting with the solution to the above question.

Given,
The average speed, excluding the stoppage, is 72 kmph.
The average speed, including the stoppage, is 60 kmph.
So, as asked in the question, let us keep our calculation limited to 1 hour.

We know, when the bus moves, its average speed is 72 kmph, and when it stops, it has an average speed of zero.

The distance covered per hour when the bus doesn’t stop is given by:
${{v}_{avg}}\times time=72\times 1=72\text{ km}$

Similarly,
The distance covered per hour when the bus does stop at the stoppages is given by:
${{v}_{avg}}\times time=60\times 1=60\text{ km}$

So, the difference in the distance per hour in both cases will be given by the absolute value of the result of subtraction of the distance covered in each case.
$\therefore 72-60=12\text{ km}$

Now, we know, the stoppage time is:
$\dfrac{\text{the difference in the distance per hour in both cases}}{\text{Average speed of moving bus}}$
$=\dfrac{12}{72}$
$=\dfrac{1}{6}\text{ hours}$
$=\dfrac{1}{6}\times 60\text{ minutes}$
$=10\text{ minutes}$

Hence, we can say that the stoppage time per hour of the bus is 10 minutes, and the answer is option (d).

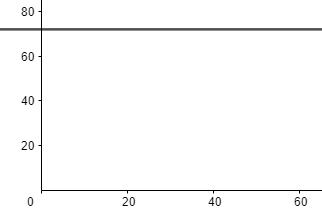
Note: An alternative solution can be using a distance vs time graph, where the area under the graph gives you the distance covered by the body.
Bus moving without stoppage can be shown as:

While the bus moving with stoppage can be shown as:

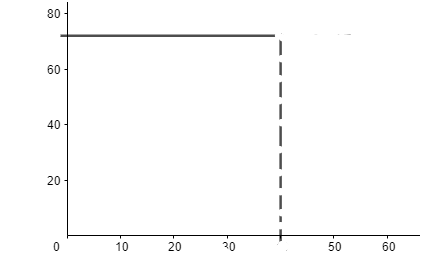
(Time in the graph is in minutes)
Here, from 0 to t is the bus moving, and from t to 60 is the stoppage.
So, the area under the graph should be equal to 60, as in this case distance travelled is 60 km.
$t\times 72=60$
$t=\dfrac{5}{6}\text{ hours = 50 minutes}$

So, stoppage time is from t to 60, which comes out to be 10 minutes.