Question

Excess pressure can be (2T/R) for
A.) Spherical drop
B.) Spherical meniscus
C.) Cylindrical bubble in air
D.) Spherical bubble in water

Answer 1

Hint: in this question we first start by finding the excess pressure for different case that is when we have one free surface that is in case of water drop excess pressure is $\dfrac{{2T}}{R}$ and when there are two free surface that is in case of water bubble in air excess pressure becomes $2 \times \dfrac{{2T}}{R} = \dfrac{{4T}}{R}$ And also know that the excess pressure for a cylindrical drop and cylindrical bubble is $\dfrac{T}{R}$ and $\dfrac{{2T}}{R}$ respectively. And using these we find that all the options will have an excess pressure equal to $\dfrac{{2T}}{R}$

Step by Step Answer:
First we will find the excess pressure for a spherical drop and for that we first draw the cross section view of a spherical drop with radius R and surface tension T as can be shown in figure 1.

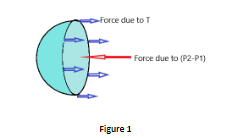
Now writing the forces acting on the drop that are
Force due to the external pressure that is ${F_{{P_1}}} = {P_1}\pi {R^2}$ acting in the right direction
Force due to the internal pressure that is ${F_{{P_2}}} = {P_2}\pi {R^2}$ acting in left direction
Force due to the surface tension that is ${F_T} = 2\pi RT$ acting in right direction
Since the drop is in equilibrium we will get

${F_{{P_1}}} + {F_T} = {F_{{P_2}}}$
$\Rightarrow {P_1}\pi {R^2} + 2\pi RT = {P_2}\pi {R^2}$
$\Rightarrow ({P_2} - {P_1})\pi {R^2} = 2\pi RT$

Hence the Excess pressure $\Delta P = {P_2} - {P_1} = \dfrac{{2T}}{R}$
Now we will find the excess pressure for a spherical bubble in water and for that we first draw the cross section view of a spherical bubble with radius R and surface tension T as can be shown in figure 2. We know that bubbles have two liquid surfaces in contact with air, one is inside the bubble and the other one is outside the bubble. So, the force due to surface tension is $2 \times \left( {2\pi RT} \right)$.

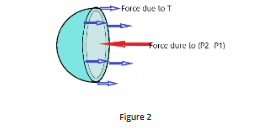
Now writing the forces acting on the drop that are
Force due to the external pressure that is ${F_{{P_1}}} = {P_1}\pi {R^2}$ acting in the right direction
Force due to the internal pressure that is ${F_{{P_2}}} = {P_2}\pi {R^2}$ acting in left direction
Force due to the surface tension that is ${F_T} = 4\pi RT$ acting in right direction
Since the drop is in equilibrium we will get

${F_{{P_1}}} + {F_T} = {F_{{P_2}}}$
$\Rightarrow {P_1}\pi {R^2} + 4\pi RT = {P_2}\pi {R^2}$
$\Rightarrow ({P_2} - {P_1})\pi {R^2} = 4\pi RT$
Hence the Excess pressure $\Delta P = {P_2} - {P_1} = \dfrac{{4T}}{R}$

Using this above two we can conclude that when we have one free surface that is in case of water drop excess pressure is $\dfrac{{2T}}{R}$ and when there are two free surface that is in case of water bubble in air excess pressure becomes $2 \times \dfrac{{2T}}{R} = \dfrac{{4T}}{R}$. The excess pressure of cylindrical surfaces is half that of spherical surfaces that is the excess pressure for a cylindrical drop and cylindrical bubble is $\dfrac{T}{R}$ and $\dfrac{{2T}}{R}$ respectively. Now looking at the options

Spherical drop will have only one free surface so excess pressure will be $\dfrac{{2T}}{R}$
Spherical meniscus will have only one free surface so excess pressure will be $\dfrac{{2T}}{R}$
Cylindrical bubble in air will have two free surface but in a cylindrical bubble the excess pressure due to one free surface is $\dfrac{T}{R}$ so here excess pressure will be $\dfrac{{2T}}{R}$
Spherical bubble in water have one free surface so excess pressure will be $\dfrac{{2T}}{R}$
Hence all the options will have an excess pressure $\dfrac{{2T}}{R}$ so all options are correct.

Note: For these types of questions we need the concept of surface tension and pressure due to the air-water interface. We also need to remember the excess pressure for different shapes of air-water interfaces that we see in real life, that is cylindrical drops and bubbles, spherical drops and bubbles, and meniscus. We need to know how excess pressure varies with the free surfaces.