Question
Question: Find the domain of the function $f(x) = \sqrt{x^2 - x - 6} + \sqrt{6 - x}$...
Find the domain of the function
f(x)=x2−x−6+6−x
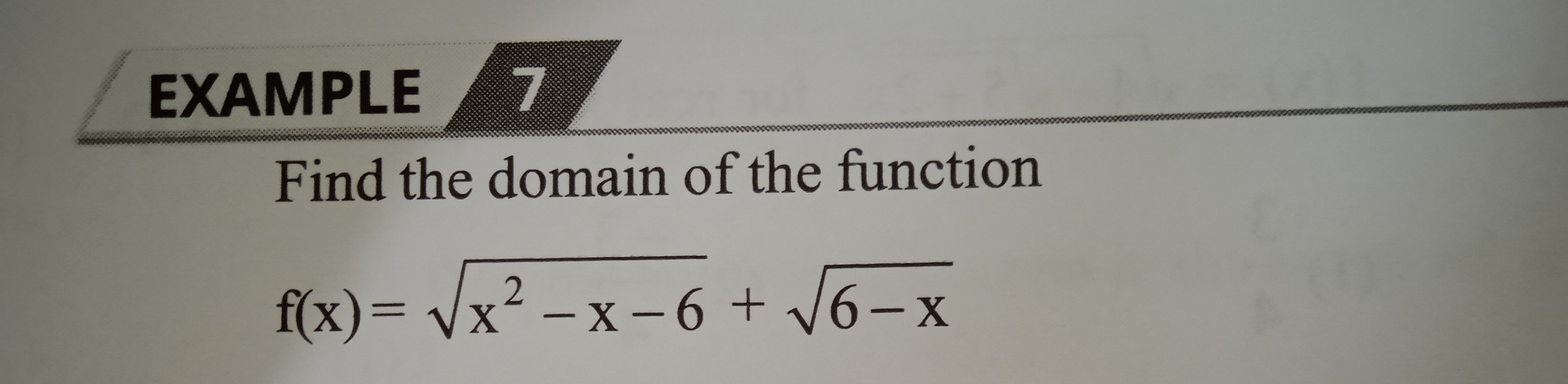
(−∞,−2]∪[3,6]
Solution
To find the domain of the function f(x)=x2−x−6+6−x, we need to ensure that both terms under the square root are non-negative.
Condition 1: The expression under the first square root must be non-negative.
x2−x−6≥0
To solve this quadratic inequality, we first find the roots of the corresponding quadratic equation x2−x−6=0.
Factoring the quadratic expression:
(x−3)(x+2)≥0
The roots are x=3 and x=−2. Since the quadratic has a positive leading coefficient (coefficient of x2 is 1), the parabola opens upwards. Thus, the expression x2−x−6 is non-negative when x is less than or equal to the smaller root or greater than or equal to the larger root.
So, x≤−2 or x≥3. In interval notation, this solution set is D1=(−∞,−2]∪[3,∞).
Condition 2: The expression under the second square root must be non-negative.
6−x≥0
6≥x
x≤6
In interval notation, this solution set is D2=(−∞,6].
Finding the Domain:
The domain of f(x) is the intersection of the solution sets from Condition 1 and Condition 2, i.e., D=D1∩D2.
We need to find the values of x that satisfy both conditions:
x∈((−∞,−2]∪[3,∞)) AND x∈(−∞,6].
Let's find the intersection of the intervals:
- Intersection of (−∞,−2] with (−∞,6]: This gives (−∞,−2].
- Intersection of [3,∞) with (−∞,6]: This gives [3,6].
Combining these two resulting intervals, the domain of f(x) is (−∞,−2]∪[3,6].
