Question

Make dual for following LPP:

Maximize Z = 3x₁ + 4x₂ Subject to x₁ + 3x₂ = 4 -x₁ + 4x₂ ≥ 2 3x₁ + 6x₂ ≤ 12 x₁ Unrestricted, x₂ ≥ 0

Answer 1

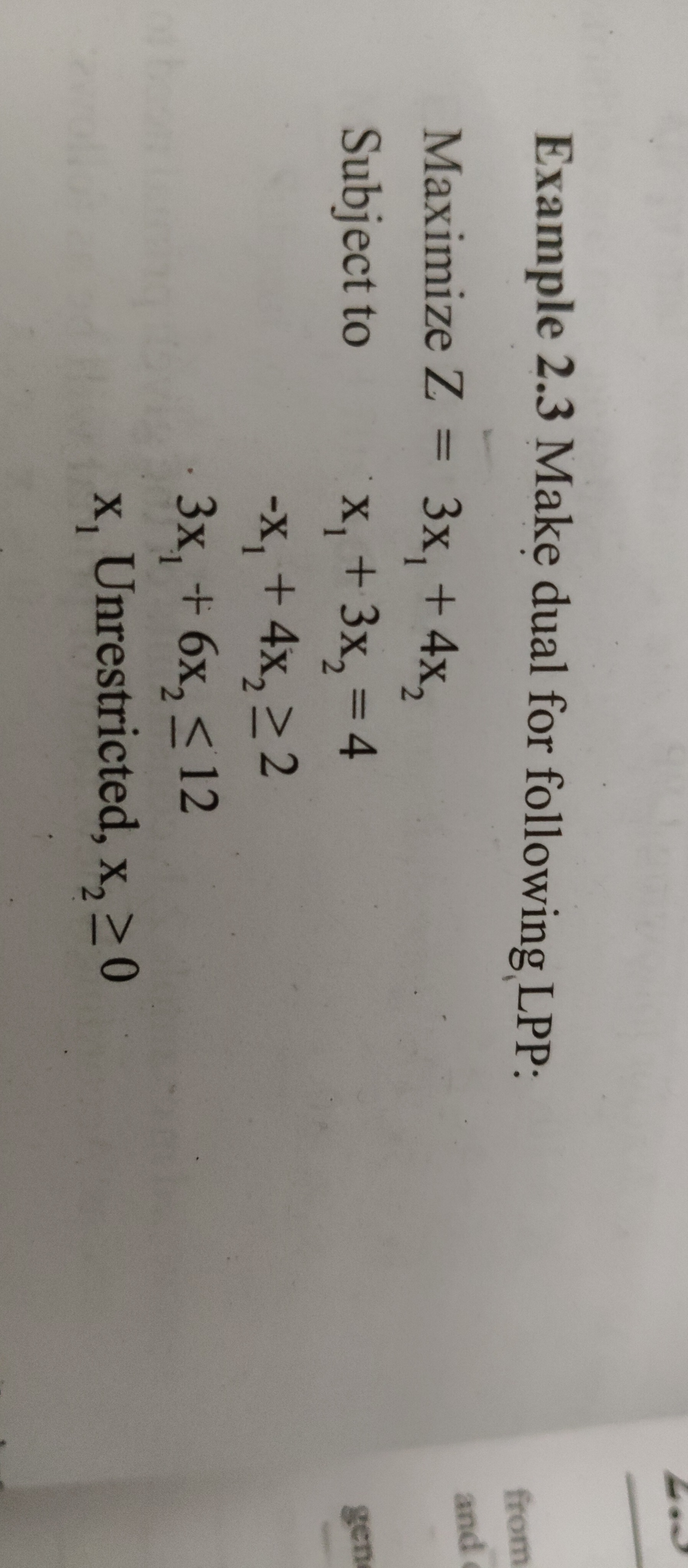
Minimize W = 4y₁ + 2y₂ + 12y₃

Subject to

y₁ - y₂ + 3y₃ = 3

3y₁ + 4y₂ + 6y₃ ≥ 4

y₁ Unrestricted, y₂ ≤ 0, y₃ ≥ 0

Answer 2

To make the dual for the given Linear Programming Problem (LPP), we follow the standard rules for primal-dual transformation.

The given primal LPP is:

Maximize Z = 3x₁ + 4x₂

Subject to

1. x₁ + 3x₂ = 4
2. -x₁ + 4x₂ ≥ 2
3. 3x₁ + 6x₂ ≤ 12

x₁ Unrestricted, x₂ ≥ 0

Rules for Primal-Dual Conversion (Primal is Max, Dual is Min):

1. Objective Function: The coefficients of the dual objective function are the right-hand side (RHS) values of the primal constraints.

2. Number of Variables and Constraints:

   • Each constraint in the primal problem corresponds to a variable in the dual problem.
   • Each variable in the primal problem corresponds to a constraint in the dual problem.

3. Coefficients of Dual Constraints: The coefficients of the dual constraints are the transpose of the coefficients of the primal variables in the constraints.

4. Sign Restrictions and Constraint Types:

   Primal Constraint Type	Dual Variable Sign
   ≤	yᵢ ≥ 0
   ≥	yᵢ ≤ 0
   =	yᵢ Unrestricted

   Primal Variable Sign	Dual Constraint Type
   xⱼ ≥ 0	≥
   xⱼ ≤ 0	≤
   xⱼ Unrestricted	=

Let's apply these rules:

Step 1: Determine the type of dual problem and dual variables.

Since the primal is a maximization problem, the dual will be a minimization problem. There are 3 constraints in the primal, so there will be 3 dual variables: y₁, y₂, y₃.

Step 2: Formulate the objective function of the dual.

The RHS values of the primal constraints are 4, 2, and 12.

Minimize W = 4y₁ + 2y₂ + 12y₃

Step 3: Formulate the constraints of the dual.

There are 2 variables in the primal, so there will be 2 dual constraints.

• First Dual Constraint (corresponding to x₁):

  The coefficients of x₁ in the primal constraints are 1, -1, and 3. The coefficient of x₁ in the primal objective function is 3. Since x₁ is unrestricted, the dual constraint for x₁ will be an equality.

  1y₁ - 1y₂ + 3y₃ = 3

• Second Dual Constraint (corresponding to x₂):

  The coefficients of x₂ in the primal constraints are 3, 4, and 6. The coefficient of x₂ in the primal objective function is 4. Since x₂ ≥ 0, the dual constraint for x₂ will be of '≥' type.

  3y₁ + 4y₂ + 6y₃ ≥ 4

Step 4: Determine the sign restrictions for the dual variables.

• y₁: Corresponds to the first primal constraint (x₁ + 3x₂ = 4), which is an equality. Therefore, y₁ is unrestricted.
• y₂: Corresponds to the second primal constraint (-x₁ + 4x₂ ≥ 2), which is of '≥' type. Therefore, y₂ ≤ 0.
• y₃: Corresponds to the third primal constraint (3x₁ + 6x₂ ≤ 12), which is of '≤' type. Therefore, y₃ ≥ 0.

Combining all these steps, the dual LPP is:

Minimize W = 4y₁ + 2y₂ + 12y₃

Subject to

y₁ - y₂ + 3y₃ = 3

3y₁ + 4y₂ + 6y₃ ≥ 4

y₁ Unrestricted, y₂ ≤ 0, y₃ ≥ 0