Solveeit Logo
Login

Question

Question: In the arrangement shown in figure, if the acceleration of B is a, then find the acceleration of A....

In the arrangement shown in figure, if the acceleration of B is a, then find the acceleration of A.

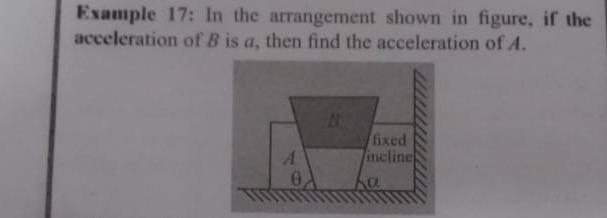
A

asin⁡(θ−α)sin⁡θ\frac{a \sin(\theta - \alpha)}{\sin \theta}

B

acos⁡(θ−α)cos⁡θ\frac{a \cos(\theta - \alpha)}{\cos \theta}

C

asin⁡(θ+α)sin⁡θ\frac{a \sin(\theta + \alpha)}{\sin \theta}

D

acos⁡(θ+α)cos⁡θ\frac{a \cos(\theta + \alpha)}{\cos \theta}

Answer

The acceleration of A is asin⁡(θ−α)sin⁡θ\frac{a \sin(\theta - \alpha)}{\sin \theta}.

Explanation

Solution

Let the acceleration of block A be a⃗A=aAi^\vec{a}_A = a_A \hat{i}. Block B moves along an inclined plane with acceleration a⃗B=a(cos⁡αi^−sin⁡αj^)\vec{a}_B = a (\cos \alpha \hat{i} - \sin \alpha \hat{j}). The acceleration of B relative to A is a⃗B/A=a⃗B−a⃗A=[acos⁡α−aA]i^−[asin⁡α]j^\vec{a}_{B/A} = \vec{a}_B - \vec{a}_A = [a \cos \alpha - a_A] \hat{i} - [a \sin \alpha] \hat{j}. The unit normal vector to the contact surface is n^=−sin⁡θi^+cos⁡θj^\hat{n} = -\sin \theta \hat{i} + \cos \theta \hat{j}. For no slipping, a⃗B/A⋅n^=0\vec{a}_{B/A} \cdot \hat{n} = 0. ([acos⁡α−aA]i^−[asin⁡α]j^)⋅(−sin⁡θi^+cos⁡θj^)=0([a \cos \alpha - a_A] \hat{i} - [a \sin \alpha] \hat{j}) \cdot (-\sin \theta \hat{i} + \cos \theta \hat{j}) = 0 (acos⁡α−aA)(−sin⁡θ)+(−asin⁡α)(cos⁡θ)=0(a \cos \alpha - a_A)(-\sin \theta) + (-a \sin \alpha)(\cos \theta) = 0 −acos⁡αsin⁡θ+aAsin⁡θ−asin⁡αcos⁡θ=0-a \cos \alpha \sin \theta + a_A \sin \theta - a \sin \alpha \cos \theta = 0 aAsin⁡θ=a(cos⁡αsin⁡θ−sin⁡αcos⁡θ)a_A \sin \theta = a (\cos \alpha \sin \theta - \sin \alpha \cos \theta) aAsin⁡θ=asin⁡(θ−α)a_A \sin \theta = a \sin(\theta - \alpha) aA=asin⁡(θ−α)sin⁡θa_A = \frac{a \sin(\theta - \alpha)}{\sin \theta}