Question
Question: If $(1+x)^n=C_0+C_1x+C_2x^2+C_3x^3+.......+C_nx^n$, then find the sum $C_0C_r+C_1C_{r+1}+C_2C_{r+2}+...
If (1+x)n=C0+C1x+C2x2+C3x3+.......+Cnxn, then find the sum C0Cr+C1Cr+1+C2Cr+2+.......+Cn−rCn
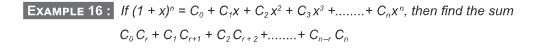
(n−r2n)
(n+r2n)
(rn)
(n−rn)
The sum is (n−r2n) or equivalently (n+r2n).
Solution
The given sum is S=C0Cr+C1Cr+1+C2Cr+2+.......+Cn−rCn. This can be written in summation notation as: S=∑k=0n−rCkCk+r
Since Ck represents the binomial coefficients, Ck=(kn). Substituting this into the sum: S=∑k=0n−r(kn)(k+rn)
Using the property of binomial coefficients (mn)=(n−mn), we can rewrite (k+rn) as (n−(k+r)n)=(n−k−rn). So, the sum becomes: S=∑k=0n−r(kn)(n−k−rn)
This sum is the coefficient of xn−r in the expansion of (1+x)n×(1+x)n=(1+x)2n. The expansion of (1+x)2n is given by: (1+x)2n=∑j=02n(j2n)xj
The coefficient of xn−r in (1+x)2n is (n−r2n). Therefore, the sum S=(n−r2n).
Using the identity (KN)=(N−KN), we can also write: (n−r2n)=(2n−(n−r)2n)=(n+r2n). Thus, the sum can also be expressed as (n+r2n).
