Question

In the figure shown,

(a) Find the force of friction acting on the block.

(b) State whether the block will move or not. If yes then with what acceleration?

Answer 1

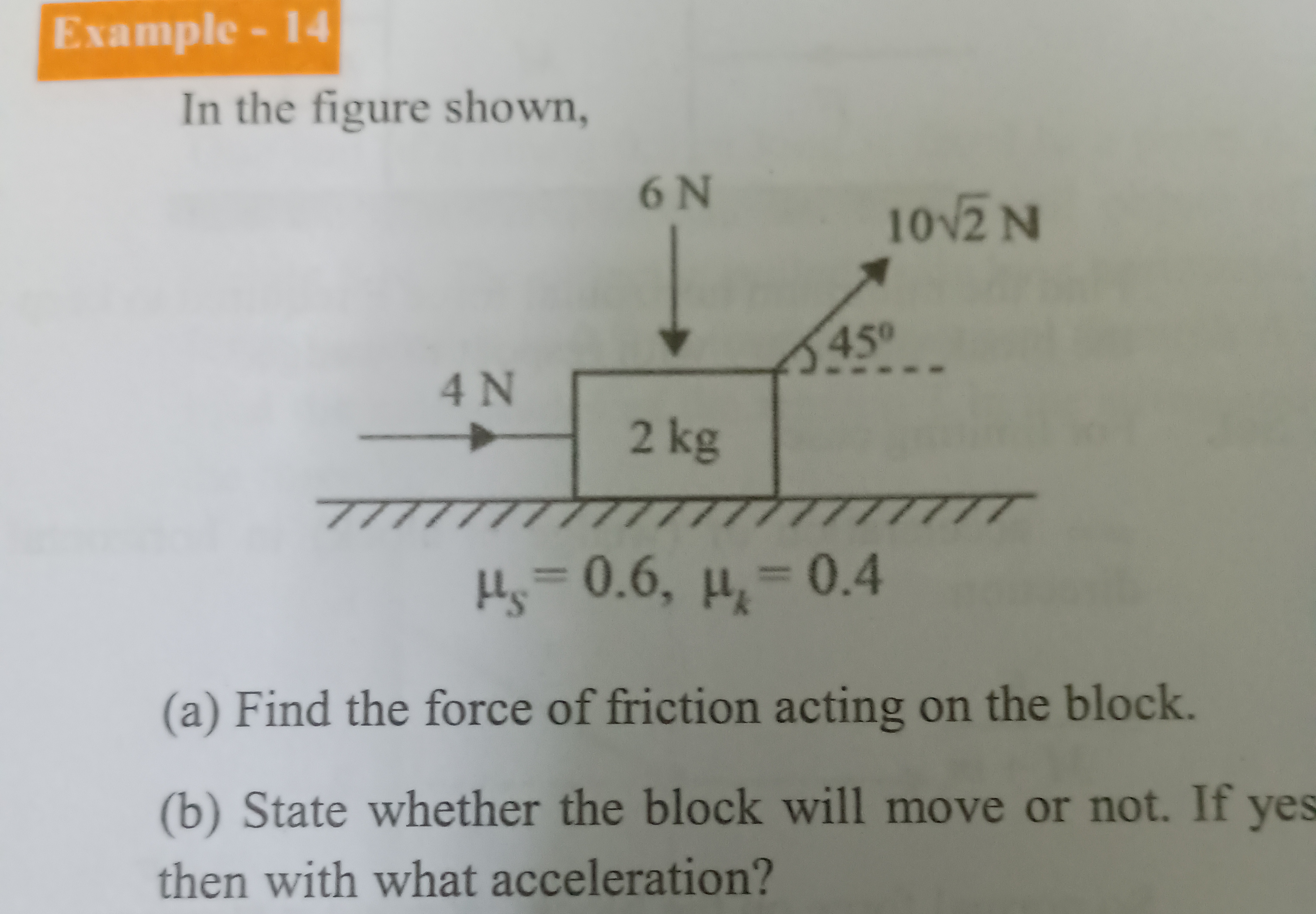
(a) The force of friction acting on the block is 6.4 N.

(b) The block will move with an acceleration of 3.8 m/s².

Answer 2

1. Resolve Forces: Decompose the $10\sqrt{2}$ N force into horizontal ($10\sqrt{2} \cos 45^\circ = 10 \text{ N}$) and vertical ($10\sqrt{2} \sin 45^\circ = 10 \text{ N}$) components.

2. Normal Force: Sum vertical forces to zero for equilibrium. Upward forces (Normal force N + 10 N) balance downward forces (Weight (2 kg * 10 m/s² = 20 N) + 6 N). This gives $N = 16 \text{ N}$.

3. Maximum Static Friction: Calculate $f_{s\_max} = \mu_s N = 0.6 \times 16 = 9.6 \text{ N}$.

4. Net Applied Horizontal Force: Sum horizontal forces acting to cause motion: $4 \text{ N} + 10 \text{ N} = 14 \text{ N}$.

5. Motion Check: Since the applied horizontal force ($14 \text{ N}$) is greater than the maximum static friction ($9.6 \text{ N}$), the block will move.

6. Kinetic Friction: As the block moves, the friction force becomes kinetic friction: $f_k = \mu_k N = 0.4 \times 16 = 6.4 \text{ N}$.

7. Acceleration: Apply Newton's second law horizontally: $F_{net} = ma$. The net force is $14 \text{ N} - 6.4 \text{ N} = 7.6 \text{ N}$. So, $a = \frac{7.6 \text{ N}}{2 \text{ kg}} = 3.8 \text{ m/s}^2$.