Question
Question: If $w = \frac{-1}{i-1}$ and $|w| = 1, I = \sqrt{-1}$ then $z$ lies on...
If w=i−1−1 and ∣w∣=1,I=−1 then z lies on
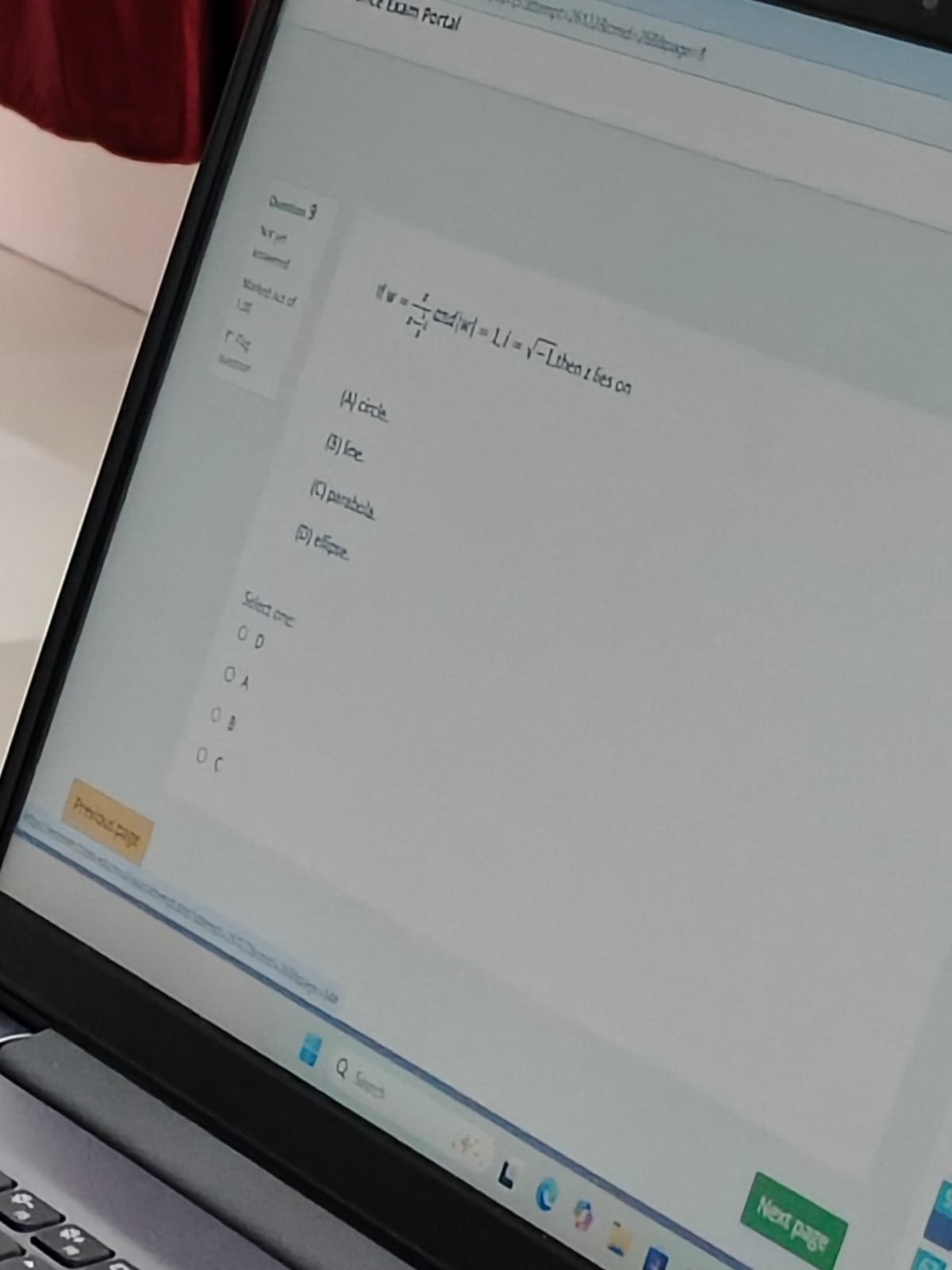
circle
line
parabola
ellipse
A
Solution
The given complex number is w=i−1−1.
First, let's simplify the expression for w:
w=i−1−1=−(1−i)−1=1−i1
To simplify, multiply the numerator and denominator by the conjugate of the denominator, which is 1+i:
w=1−i1×1+i1+i=(1)2−(i)21+i
Since i2=−1:
w=1−(−1)1+i=1+11+i=21+i
So, w=21+21i.
Now, let's calculate the modulus of this complex number w:
∣w∣=21+21i=(21)2+(21)2
∣w∣=41+41=42=21
∣w∣=21.
The problem statement says "If w=i−1−1 and ∣w∣=1".
Our calculation shows that if w=i−1−1, then ∣w∣=21.
Since 21=1, there is a contradiction in the problem statement. The premise "w=i−1−1 and ∣w∣=1" is false.
Furthermore, the question asks "then z lies on", but the variable z is not defined anywhere in the problem statement.
Given the options (circle, line, parabola, ellipse), which are all loci of points, and the common types of problems involving complex numbers, it is highly probable that there is a typo in the question. The most reasonable interpretation that leads to a sensible answer from the given options is that the question intended to ask about the locus of z such that ∣z∣=1. This would mean the "w" in "∣w∣=1" was a typo for "z", and the expression for w is either irrelevant or a distractor.
Assuming the question intended to ask for the locus of z such that ∣z∣=1:
Let z=x+iy, where x and y are real numbers.
The condition ∣z∣=1 means the distance of the complex number z from the origin (0,0) in the complex plane is 1.
Mathematically, ∣z∣=x2+y2.
So, x2+y2=1.
Squaring both sides, we get:
x2+y2=1
This is the standard equation of a circle centered at the origin (0,0) with a radius of 1.
Therefore, if ∣z∣=1, z lies on a circle.
