Question
Question: Evaluate $\lim_{x\to 0}\left( \frac{1-\sqrt[3]{x^2+1}}{x^2} \right)$...
Evaluate limx→0(x21−3x2+1)
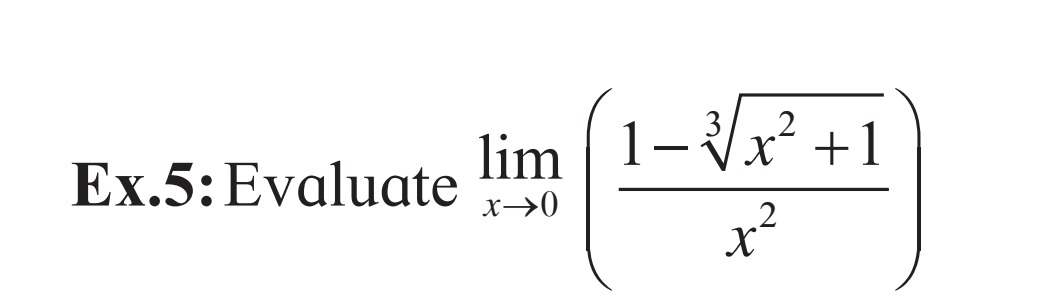
Answer
The limit evaluates to −31.
Explanation
Solution
The limit is of the indeterminate form 00. We used algebraic manipulation involving the difference of cubes identity a3−b3=(a−b)(a2+ab+b2) to rationalize the numerator. By setting a=1 and b=(x2+1)1/3, we multiplied the numerator and denominator by a2+ab+b2=1+(x2+1)1/3+(x2+1)2/3. This transformed the numerator into a3−b3=1−(x2+1)=−x2. After canceling x2 from the numerator and denominator (for x=0), the expression simplified to 1+(x2+1)1/3+(x2+1)2/3−1. Evaluating the limit as x→0 by direct substitution gives 1+1+1−1=−31.
Alternatively, L'Hopital's Rule could be applied.
