Solveeit Logo
Login

Question

Question: Find the vector equation of the line passing through the point having position vector $2\hat{i} + \h...

Find the vector equation of the line passing through the point having position vector 2i^+j^−3k^2\hat{i} + \hat{j} - 3\hat{k} and perpendicular to vectors i^+j^+k^\hat{i} + \hat{j} + \hat{k} and i^+2j^−k^\hat{i} + 2\hat{j} - \hat{k}.

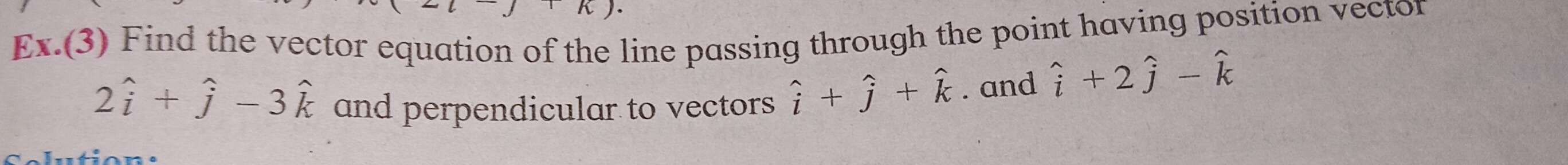
Answer

r⃗=(2i^+j^−3k^)+t(−3i^+2j^+k^),t∈R\vec{r} = (2\hat{i} + \hat{j} - 3\hat{k}) + t(-3\hat{i} + 2\hat{j} + \hat{k}), \quad t \in \mathbb{R}

Explanation

Solution

To find the vector equation of the line:

  1. Find the Direction Vector:

    The line is perpendicular to both a⃗=i^+j^+k^\vec{a} = \hat{i} + \hat{j} + \hat{k} and b⃗=i^+2j^−k^\vec{b} = \hat{i} + 2\hat{j} - \hat{k}. The direction vector d⃗\vec{d} is given by the cross product:

    d⃗=a⃗×b⃗=∣i^j^k^11112−1∣\vec{d} = \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 1 \\ 1 & 2 & -1 \end{vmatrix}

    Compute its components:

    • dx=(1)(−1)−(1)(2)=−1−2=−3d_x = (1)(-1) - (1)(2) = -1 - 2 = -3
    • dy=−[(1)(−1)−(1)(1)]=−(−1−1)=2d_y = -\Big[(1)(-1) - (1)(1)\Big] = -(-1 - 1)= 2
    • dz=(1)(2)−(1)(1)=2−1=1d_z = (1)(2) - (1)(1) = 2 - 1 = 1

    Thus, d⃗=−3i^+2j^+k^\vec{d} = -3\hat{i} + 2\hat{j} + \hat{k}.

  2. Write the Vector Equation of the Line:

    The line passes through the point with position vector r0⃗=2i^+j^−3k^\vec{r_0} = 2\hat{i} + \hat{j} - 3\hat{k}, and has direction vector d⃗\vec{d}. Therefore, the vector equation is:

    r⃗=r0⃗+t d⃗=(2i^+j^−3k^)+t(−3i^+2j^+k^),t∈R\vec{r} = \vec{r_0} + t\,\vec{d} = (2\hat{i} + \hat{j} - 3\hat{k}) + t(-3\hat{i} + 2\hat{j} + \hat{k}), \quad t \in \mathbb{R}