Question

Find the angle between the line $\overline{r} = (\hat{i} + 2\hat{j} + \hat{k}) + \lambda(\hat{i} + \hat{j} + \hat{k})$ and the plane $\overline{r}.(2\hat{i} - \hat{j} + \hat{k}) = 8$

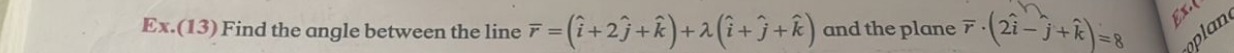
Answer 1

$\alpha = \sin^{-1}\left(\frac{\sqrt{2}}{3}\right)$

Answer 2

1. The given line has direction vector

   $$\vec{d} = \langle 1, 1, 1 \rangle.$$

2. The given plane has normal vector

   $$\vec{n} = \langle 2, -1, 1 \rangle.$$

3. The angle $\theta$ between the direction vector and the normal is given by

   $$\cos\theta = \frac{\vec{d}\cdot\vec{n}}{|\vec{d}||\vec{n}|}.$$

   Compute:

   $$\vec{d}\cdot\vec{n} = (1)(2) + (1)(-1) + (1)(1) = 2-1+1 = 2,$$ $$|\vec{d}| = \sqrt{1^2+1^2+1^2} = \sqrt{3},$$ $$|\vec{n}| = \sqrt{2^2+(-1)^2+1^2} = \sqrt{4+1+1} = \sqrt{6}.$$

   So,

   $$\cos\theta = \frac{2}{\sqrt{3}\sqrt{6}} = \frac{2}{\sqrt{18}} = \frac{2}{3\sqrt{2}} = \frac{\sqrt{2}}{3}.$$

4. The angle between the line and the plane, $\alpha$, is the complement of $\theta$ (since the normal is perpendicular to the plane):

   $$\alpha = 90^\circ - \theta.$$

   Alternatively, using trigonometric identity:

   $$\sin\alpha = \cos\theta = \frac{\sqrt{2}}{3}.$$

   Thus,

   $$\alpha = \sin^{-1}\left(\frac{\sqrt{2}}{3}\right).$$