Question

Let $f:N\rightarrow R$ such that $\sum_{r=1}^{n} rf(r) = n(n+1)f(n) \forall n>1$

If $f(1)=1$ find Value of $f(1012)=$

Answer 1

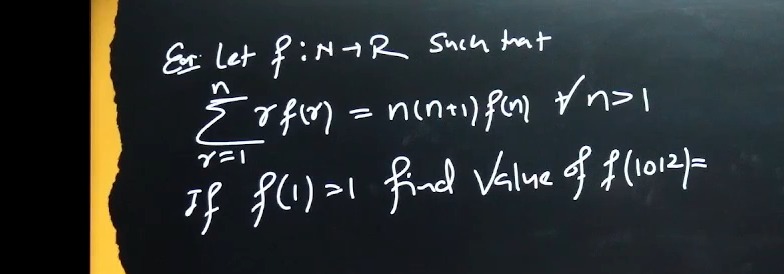
The value of $f(1012)$ is $\frac{1}{2024}$.

Answer 2

Let $S_n = \sum_{r=1}^{n} rf(r)$. The given relation is $S_n = n(n+1)f(n)$ for $n > 1$. We also know that $S_n = S_{n-1} + nf(n)$ for $n > 1$.

For $n > 2$, we can substitute the given relation into $S_n = S_{n-1} + nf(n)$: $n(n+1)f(n) = (n-1)n f(n-1) + nf(n)$

Dividing by $n$ (since $n > 2$, $n \neq 0$): $(n+1)f(n) = (n-1)f(n-1) + f(n)$ $nf(n) = (n-1)f(n-1)$ This gives the recurrence relation $f(n) = \frac{n-1}{n}f(n-1)$ for $n \geq 3$.

To find $f(2)$, we use the original relation for $n=2$: $S_2 = \sum_{r=1}^{2} rf(r) = 1 \cdot f(1) + 2 \cdot f(2)$. The given relation states $S_2 = 2(2+1)f(2) = 6f(2)$. So, $f(1) + 2f(2) = 6f(2)$. Given $f(1)=1$, we have $1 + 2f(2) = 6f(2)$, which simplifies to $1 = 4f(2)$, so $f(2) = \frac{1}{4}$.

Now we solve the recurrence relation $f(n) = \frac{n-1}{n}f(n-1)$ for $n \geq 3$: $f(n) = \frac{n-1}{n} \cdot f(n-1)$ $f(n) = \frac{n-1}{n} \cdot \frac{n-2}{n-1} \cdot f(n-2)$ $f(n) = \frac{n-1}{n} \cdot \frac{n-2}{n-1} \cdot \frac{n-3}{n-2} \cdots \frac{2}{3} f(2)$

This is a telescoping product, which simplifies to: $f(n) = \frac{2}{n} f(2)$ for $n \geq 3$.

Substitute the value of $f(2) = \frac{1}{4}$: $f(n) = \frac{2}{n} \cdot \frac{1}{4} = \frac{1}{2n}$ for $n \geq 3$.

Let's check if this formula holds for $n=2$: $f(2) = \frac{1}{2 \cdot 2} = \frac{1}{4}$, which matches our calculated value. Therefore, the function can be defined as: $f(1) = 1$ $f(n) = \frac{1}{2n}$ for $n \geq 2$.

We need to find $f(1012)$. Since $1012 \geq 2$, we use the formula $f(n) = \frac{1}{2n}$: $f(1012) = \frac{1}{2 \cdot 1012} = \frac{1}{2024}$.