Question
Question: Ex. Given an equilateral triangle with side $l$. Find electric field strength at the centroid. The l...
Ex. Given an equilateral triangle with side l. Find electric field strength at the centroid. The linear charge density is as shown in figure.
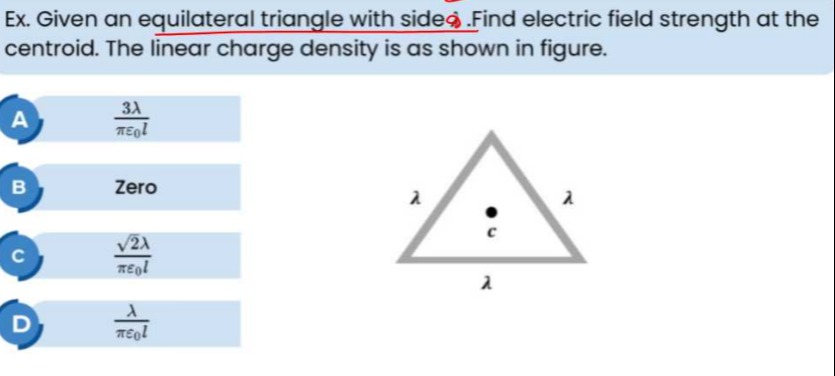
πϵ0l3λ
Zero
πϵ0l2λ
πϵ0lλ
Zero
Solution
The electric field at the centroid of an equilateral triangle with uniformly distributed charge on its sides can be calculated by considering the contribution from each side. Let the side length of the equilateral triangle be l and the linear charge density on each side be λ. The centroid is equidistant from each side. The distance from the centroid to each side is the inradius of the equilateral triangle, which is r=23l.
Consider one side of the triangle. The centroid is located on the perpendicular bisector of this side. The electric field at a point P at a perpendicular distance d from the midpoint of a uniformly charged rod of length l with linear charge density λ is given by E=4πϵ01d2λsinθ, where 2θ is the angle subtended by the rod at the point P. In our case, the point is the centroid, the rod is a side of length l, and the perpendicular distance is d=r=23l. The angle subtended by each half of the side at the centroid is 60∘, so 2θ=120∘ and θ=60∘.
The magnitude of the electric field at the centroid due to one side is E1=4πϵ01r2λsin60∘=4πϵ01l/(23)2λ23=4πϵ01l43λ23=4πϵ01l6λ=2πϵ0l3λ.
The direction of the electric field due to a uniformly charged line segment at a point on its perpendicular bisector is along the perpendicular bisector, pointing away from the line if the charge is positive.
Let the three sides be S1, S2, and S3. The electric fields at the centroid due to these sides are E1, E2, and E3. The magnitude of each field is E1. The direction of each field is perpendicular to the corresponding side and points away from the side. The perpendiculars from the centroid to the sides are along the lines joining the centroid to the midpoints of the sides. These lines make angles of 120∘ with each other.
Let's place the centroid at the origin. Let the direction of E1 be along the positive y-axis. Then its direction vector is (0,1). The directions of E2 and E3 are at angles of 120∘ and 240∘ with the direction of E1. So, the direction vector of E2 makes an angle of 90∘+120∘=210∘ with the positive x-axis, or an angle of 120∘ with the positive y-axis. Its components are E1cos(210∘)=−E1cos30∘=−E123 and E1sin(210∘)=−E1sin30∘=−E121. The direction vector of E3 makes an angle of 90∘+240∘=330∘ with the positive x-axis, or an angle of 240∘ with the positive y-axis. Its components are E1cos(330∘)=E1cos30∘=E123 and E1sin(330∘)=−E1sin30∘=−E121.
The total electric field is the vector sum: E=E1+E2+E3 E=(0,E1)+(−23E1,−21E1)+(23E1,−21E1) E=(0−23E1+23E1,E1−21E1−21E1) E=(0,E1−E1)=(0,0)
Thus, the total electric field strength at the centroid is zero. This result is expected due to the symmetry of the equilateral triangle and the uniform charge distribution on its sides. The electric fields due to the three sides cancel each other out vectorially at the centroid.
