Question

Ex① $f(x) = \frac{\pi}{9} - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x} = (kn(x)). Cos3x$ $x \neq \frac{\pi}{18}, \frac{\pi}{6}, \frac{\pi}{2}, \dots$ $x \neq \frac{\pi}{9}, \frac{\pi}{3}, \pi, \dots$

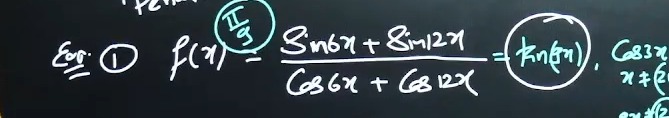
• A. kn(x) = \frac{1}{Cos3x} \left( \frac{\pi}{9} - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x} \right)
• B. kn(x) = \frac{\pi}{9Cos3x} - \frac{Sin3x(32Cos^23x - 15)}{Cos9xCos3x}
• C. kn(x) = \frac{\pi}{9} - \frac{Sin3x(32Cos^23x - 15)}{Cos9xCos3x}
• D. kn(x) = \frac{\pi}{9} \cdot Cos3x - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x}

Answer 1

Answer: (A), (B)

kn(x) = \frac{1}{Cos3x} \left( \frac{\pi}{9} - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x} \right)

Answer 2

The problem asks to express $kn(x)$ given the equation $f(x) = \frac{\pi}{9} - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x} = kn(x) \cdot Cos3x$.

To find $kn(x)$, we can rearrange the given equation: $kn(x) = \frac{f(x)}{Cos3x}$ Substituting the expression for $f(x)$: $kn(x) = \frac{1}{Cos3x} \left( \frac{\pi}{9} - \frac{Sin6x + 8Sin12x}{Cos6x + Cos12x} \right)$

This is the direct algebraic solution for $kn(x)$.

Further simplification of the fraction $\frac{Sin6x + 8Sin12x}{Cos6x + Cos12x}$ can be performed: Using sum-to-product for the denominator: $Cos6x + Cos12x = 2Cos\left(\frac{6x+12x}{2}\right)Cos\left(\frac{6x-12x}{2}\right) = 2Cos(9x)Cos(-3x) = 2Cos(9x)Cos(3x)$.

For the numerator, using double angle identities: $Sin6x = 2Sin3xCos3x$ $Sin12x = 2Sin6xCos6x$ $Sin6x + 8Sin12x = Sin6x + 8(2Sin6xCos6x) = Sin6x(1 + 16Cos6x)$ Substitute $Sin6x = 2Sin3xCos3x$: Numerator = $2Sin3xCos3x(1 + 16Cos6x)$

The fraction becomes: $\frac{2Sin3xCos3x(1 + 16Cos6x)}{2Cos9xCos3x}$ Assuming $Cos3x \neq 0$, we can cancel $2Cos3x$: $\frac{Sin3x(1 + 16Cos6x)}{Cos9x}$ Using $Cos6x = 2Cos^23x - 1$: $1 + 16Cos6x = 1 + 16(2Cos^23x - 1) = 1 + 32Cos^23x - 16 = 32Cos^23x - 15$. So the fraction simplifies to $\frac{Sin3x(32Cos^23x - 15)}{Cos9x}$.

Substituting this back into the expression for $kn(x)$: $kn(x) = \frac{1}{Cos3x} \left( \frac{\pi}{9} - \frac{Sin3x(32Cos^23x - 15)}{Cos9x} \right)$ $kn(x) = \frac{\pi}{9Cos3x} - \frac{Sin3x(32Cos^23x - 15)}{Cos9xCos3x}$

Both forms are valid representations of $kn(x)$. The first option is the most direct answer derived from rearranging the equation. The second option is the result after simplifying the trigonometric fraction. The question asks for the value of $kn(x)$, and the first option is the most direct and unsimplified representation.

The constraints $x \neq (2$ and $8x \neq (2$ in the original question are incomplete. Assuming they are meant to ensure the denominators are non-zero, typical constraints for this expression would be $Cos6x + Cos12x \neq 0$ and $Cos3x \neq 0$. This implies $2Cos9xCos3x \neq 0$, so $Cos9x \neq 0$ and $Cos3x \neq 0$. $3x \neq \frac{\pi}{2} + n\pi \implies x \neq \frac{\pi}{6} + \frac{n\pi}{3}$ $9x \neq \frac{\pi}{2} + n\pi \implies x \neq \frac{\pi}{18} + \frac{n\pi}{9}$ These correspond to the corrected constraints in the content field.