Question
Question: Ex. 8) If $\sin A + \sin B = x$ and $\cos A + \cos B = y$ then show that $\sin (A+B) = \frac{2xy}{x^...
Ex. 8) If sinA+sinB=x and cosA+cosB=y then show that sin(A+B)=x2+y22xy
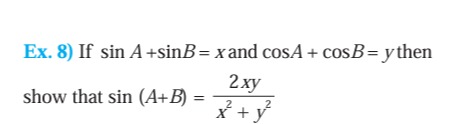
Answer
sin(A+B)=x2+y22xy
Explanation
Solution
Solution:
Express the sums using the sum‐to‐product formulas:
sinA+sinB=2sin2A+Bcos2A−B=x,cosA+cosB=2cos2A+Bcos2A−B=y.Then,
x2+y2=4cos22A−B(sin22A+B+cos22A+B)=4cos22A−B.Next, multiply x and y:
xy=(2sin2A+Bcos2A−B)(2cos2A+Bcos2A−B)=4sin2A+Bcos2A+Bcos22A−B.Recall the double-angle formula:
sin(A+B)=2sin2A+Bcos2A+B.Thus,
xy=2sin(A+B)cos22A−B.Now substitute for cos22A−B from the expression for x2+y2:
cos22A−B=4x2+y2.So,
xy=2sin(A+B)⋅4x2+y2=21sin(A+B)(x2+y2).Finally, solving for sin(A+B):
sin(A+B)=x2+y22xy.Core Explanation:
- Write sums using sum‐to‐product formulas.
- Compute x2+y2=4cos22A−B.
- Multiply x and y and express in terms of sin(A+B).
- Substitute and simplify to obtain the result.
