Question

Evaluate: $\lim_{x \to 0} \frac{21^x-7^x-3^x+1}{x \log(1+x)}$

Answer 1

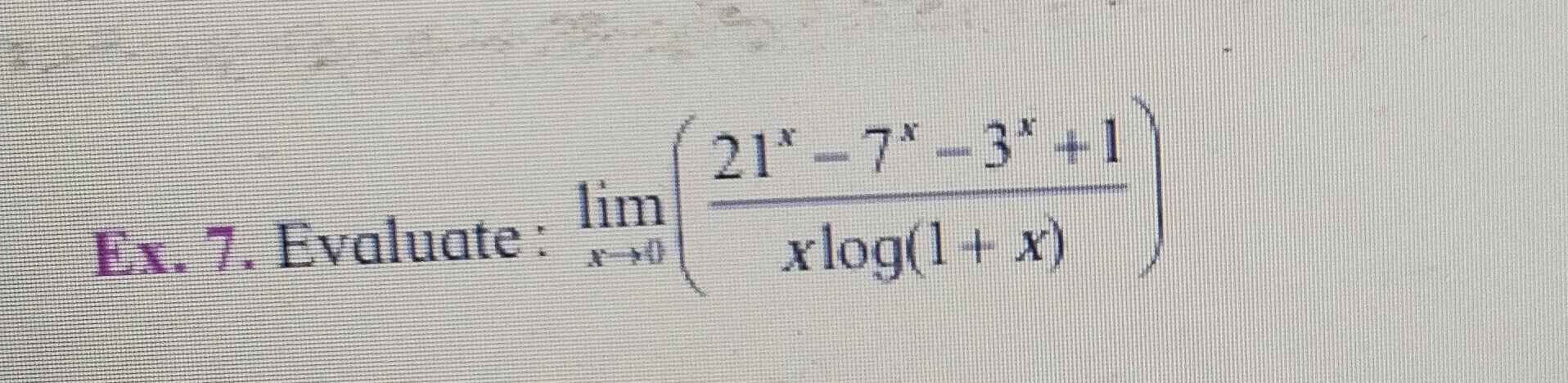
$\log 7 \log 3$

Answer 2

The given limit is $\lim_{x \to 0} \frac{21^x-7^x-3^x+1}{x \log(1+x)}$.

First, we check the form of the limit as $x \to 0$: Numerator: $21^0 - 7^0 - 3^0 + 1 = 1 - 1 - 1 + 1 = 0$. Denominator: $0 \cdot \log(1+0) = 0 \cdot \log(1) = 0 \cdot 0 = 0$. This is a $\frac{0}{0}$ indeterminate form, so we can use algebraic manipulation or L'Hopital's Rule. Algebraic manipulation using standard limits is often simpler.

Step 1: Factor the numerator.

The numerator is $21^x - 7^x - 3^x + 1$. We can write $21^x$ as $(7 \cdot 3)^x = 7^x 3^x$. So, the numerator becomes $7^x 3^x - 7^x - 3^x + 1$. This expression is in the form $ab - a - b + 1$, which factors as $(a-1)(b-1)$. Here, $a = 7^x$ and $b = 3^x$. Therefore, $7^x 3^x - 7^x - 3^x + 1 = (7^x - 1)(3^x - 1)$.

Step 2: Rewrite the limit expression using the factored numerator.

The limit becomes: $\lim_{x \to 0} \frac{(7^x - 1)(3^x - 1)}{x \log(1+x)}$

Step 3: Separate the terms to match standard limits.

We know the following standard limits:

1. $\lim_{x \to 0} \frac{a^x - 1}{x} = \log a$ (where $\log$ denotes the natural logarithm, $\ln$)
2. $\lim_{x \to 0} \frac{\log(1+x)}{x} = 1$

We can rewrite the expression as a product of terms that correspond to these standard limits: $\frac{(7^x - 1)(3^x - 1)}{x \log(1+x)} = \frac{7^x - 1}{x} \cdot \frac{3^x - 1}{x} \cdot \frac{x}{\log(1+x)}$

Step 4: Apply the limits to each term.

$\lim_{x \to 0} \frac{7^x - 1}{x} = \log 7$ $\lim_{x \to 0} \frac{3^x - 1}{x} = \log 3$ $\lim_{x \to 0} \frac{x}{\log(1+x)} = \frac{1}{\lim_{x \to 0} \frac{\log(1+x)}{x}} = \frac{1}{1} = 1$

Step 5: Multiply the results.

The overall limit is the product of these individual limits: $(\log 7) \cdot (\log 3) \cdot 1 = \log 7 \log 3$

The final answer is $\boxed{\log 7 \log 3}$.

Explanation of the solution:

The limit is of the $\frac{0}{0}$ form. The numerator $21^x-7^x-3^x+1$ is factored as $(7^x-1)(3^x-1)$. The expression is then rearranged as $\frac{7^x-1}{x} \cdot \frac{3^x-1}{x} \cdot \frac{x}{\log(1+x)}$. Applying the standard limits $\lim_{x \to 0} \frac{a^x-1}{x} = \log a$ and $\lim_{x \to 0} \frac{\log(1+x)}{x} = 1$, the limit evaluates to $(\log 7)(\log 3)(1) = \log 7 \log 3$.