Question
Question: Evaluate: $\lim_{x \to 0} (\frac{21^x - 7^x - 3^x + 1}{x\log(1+x)})$...
Evaluate: limx→0(xlog(1+x)21x−7x−3x+1)
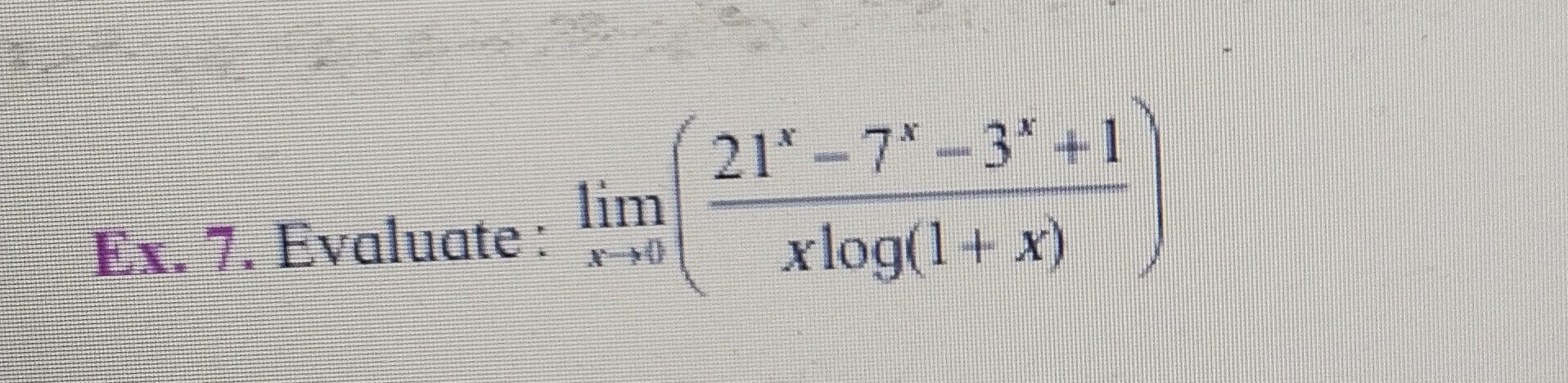
Answer
log7log3
Explanation
Solution
The limit is in 00 form. The numerator 21x−7x−3x+1 is factored as (7x−1)(3x−1). The expression is then rewritten as a product of terms: (x7x−1)⋅(x3x−1)⋅(log(1+x)x). Using standard limits limx→0xax−1=loga and limx→0xlog(1+x)=1, the limit evaluates to (log7)⋅(log3)⋅1=log7log3.
