Question

Evaluate: $\lim_{x\to 0}\left(\frac{e^{2x}+e^{-2x}-2}{x \sin x}\right)$

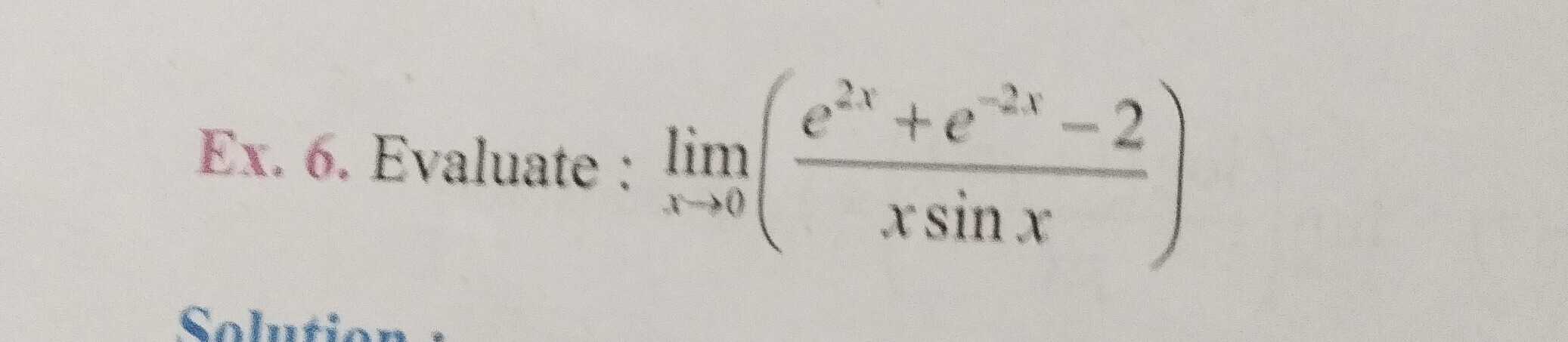
• A. 0
• B. 1
• C. 2
• D. 4

Answer 1

Answer: (D)

4

Answer 2

The limit is of the form $\frac{0}{0}$ when $x=0$.

Step 1: Simplify the numerator using an algebraic identity.

Notice that the numerator $e^{2x}+e^{-2x}-2$ resembles the expansion of $(a-b)^2$. Let $a=e^x$ and $b=e^{-x}$. Then $(e^x - e^{-x})^2 = e^{2x} + e^{-2x} - 2$.

The limit expression becomes:

$$\lim_{x\to 0}\left(\frac{(e^x - e^{-x})^2}{x \sin x}\right)$$

Step 2: Utilize standard limits.

We know the following standard limits:

1. $\lim_{u \to 0} \frac{\sin u}{u} = 1$
2. $\lim_{u \to 0} \frac{e^u - 1}{u} = 1$

Let's evaluate $\lim_{x \to 0} \frac{e^x - e^{-x}}{x}$:

$$\lim_{x \to 0} \frac{e^x - e^{-x}}{x} = \lim_{x \to 0} \left( \frac{e^x - 1}{x} - \frac{e^{-x} - 1}{x} \right) = 1 - (-1) = 2$$

Step 3: Rewrite the limit expression and evaluate.

We can rewrite the original limit expression:

$$\lim_{x\to 0}\left(\frac{(e^x - e^{-x})^2}{x \sin x}\right) = \lim_{x\to 0}\left(\frac{\left(\frac{e^x - e^{-x}}{x}\right)^2}{\frac{\sin x}{x}}\right) = \frac{\left(\lim_{x\to 0}\frac{e^x - e^{-x}}{x}\right)^2}{\lim_{x\to 0}\frac{\sin x}{x}} = \frac{(2)^2}{1} = 4$$

The final answer is 4.