Question
Question: Evaluate : $\lim_{x\to 0} \left[ \frac{\log 4 + \log(0.25+x)}{x} \right]$...
Evaluate : limx→0[xlog4+log(0.25+x)]
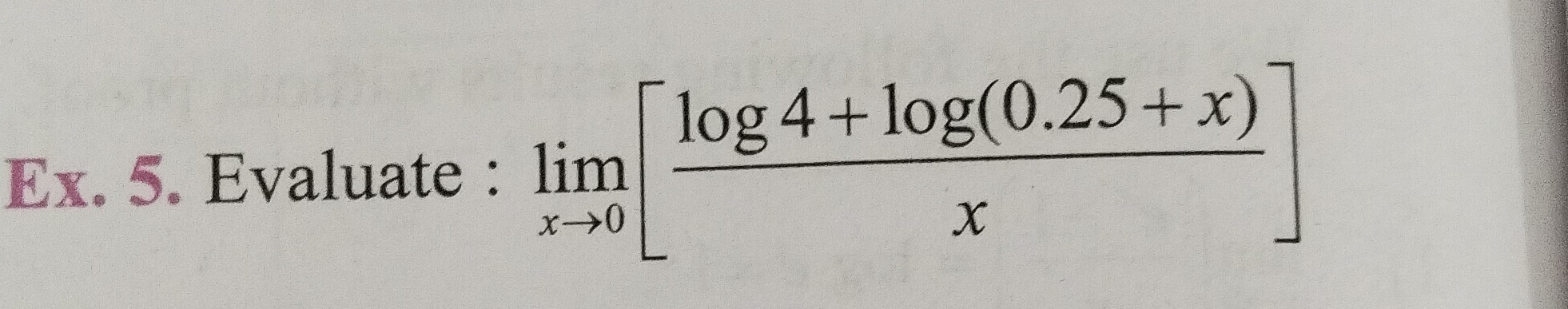
4
Solution
The problem asks to evaluate the limit: limx→0[xlog4+log(0.25+x)]
We assume log denotes the natural logarithm (ln), which is standard in calculus unless specified otherwise.
Step 1: Simplify the numerator using logarithm properties. The numerator is log4+log(0.25+x). Using the logarithm property logA+logB=log(AB): log4+log(0.25+x)=log(4×(0.25+x)) =log(4×41+4x) =log(1+4x)
Step 2: Rewrite the limit expression. Substitute the simplified numerator back into the limit: limx→0[xlog(1+4x)]
Step 3: Evaluate the limit. As x→0, the numerator log(1+4x)→log(1)=0. As x→0, the denominator x→0. This is an indeterminate form of type 00. We can use either the standard limit formula or L'Hopital's Rule.
Method 1: Using the Standard Limit Formula We know the standard limit formula: limy→0ylog(1+y)=1. To apply this, we need the term in the denominator to match the argument of the logarithm. In our case, the argument is 4x. So, we multiply and divide the expression by 4: limx→0[xlog(1+4x)]=limx→0[4xlog(1+4x)×4] Let y=4x. As x→0, y→0. The limit becomes: 4×limy→0ylog(1+y)=4×1=4
Method 2: Using L'Hopital's Rule Since the limit is of the 00 form, we can apply L'Hopital's Rule. Let f(x)=log(1+4x) and g(x)=x. Find the derivatives of f(x) and g(x): f′(x)=dxd(log(1+4x))=1+4x1×dxd(1+4x)=1+4x4 g′(x)=dxd(x)=1 Apply L'Hopital's Rule: limx→0[g′(x)f′(x)]=limx→0[11+4x4] =limx→0[1+4x4] Now, substitute x=0: =1+4(0)4=14=4
Both methods yield the same result.
The expression is simplified using logarithm properties to xlog(1+4x). This is a standard limit form limy→0ylog(1+y)=1. By multiplying and dividing by 4, the limit is transformed to 4×lim4x→04xlog(1+4x), which evaluates to 4×1=4. Alternatively, L'Hopital's Rule can be applied to the 00 form, yielding the same result.
