Question
Question: Evaluate : $\lim_{x \to 0} \left[ 1 + \frac{5x}{6} \right]^{\frac{1}{x}}$...
Evaluate : limx→0[1+65x]x1
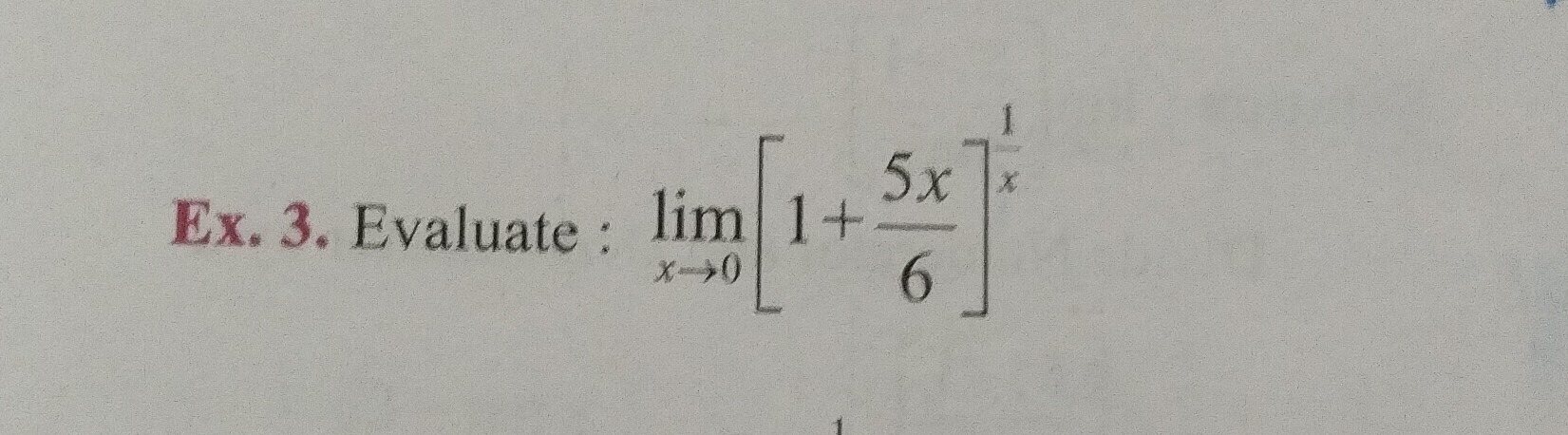
Answer
e5/6
Explanation
Solution
The limit is of the form limx→0[1+65x]x1.
This is an indeterminate form of type 1∞.
Using the standard limit formula limx→0(1+ax)1/x=ea, we compare the given limit with this form.
Here, a=65.
Therefore, the value of the limit is e5/6.
