Solveeit Logo
Login

Question

Question: Evaluate the series, $^{14}C_{14}$ $^{20}C_{10}$+$^{15}C_{14}$ $^{19}C_{10}$+$^{16}C_{14}$ $^{18}C_{...

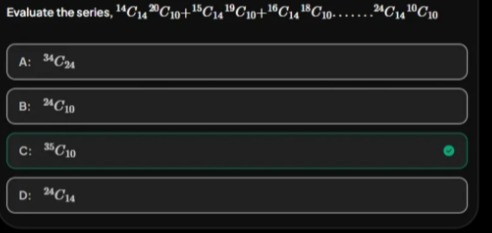
Evaluate the series, 14C14^{14}C_{14} 20C10^{20}C_{10}+15C14^{15}C_{14} 19C10^{19}C_{10}+16C14^{16}C_{14} 18C10^{18}C_{10}.......24C14^{24}C_{14} 10C10^{10}C_{10}

A

34C24^{34}C_{24}

B

24C10^{24}C_{10}

C

35C10^{35}C_{10}

D

24C14^{24}C_{14}

Answer

35C10^{35}C_{10}

Explanation

Solution

The given series is S=∑k=01014+kC1420−kC10S = \sum_{k=0}^{10} {^{14+k}C_{14}} {^{20-k}C_{10}}.

This series matches the form of the identity ∑k=0n(r+kr)(s+n−ks)=(r+s+n+1n)\sum_{k=0}^{n} {r+k \choose r} {s+n-k \choose s} = {r+s+n+1 \choose n}.

Comparing the terms 14+kC1420−kC10{^{14+k}C_{14}} {^{20-k}C_{10}} with (r+kr)(s+n−ks){r+k \choose r} {s+n-k \choose s}, we identify r=14r=14, s=10s=10, and n=10n=10.

The sum is ∑k=010(14+k14)(10+10−k10)\sum_{k=0}^{10} {14+k \choose 14} {10+10-k \choose 10}.

This corresponds to the identity with r=14r=14, s=10s=10, n=10n=10.

The value of the sum is (r+s+n+1n)=(14+10+10+110)=(3510){r+s+n+1 \choose n} = {14+10+10+1 \choose 10} = {35 \choose 10}.

Therefore, the final answer is 35C10^{35}C_{10}.