Question
Question: Evaluate the limit: $\lim_{x \to 0} \frac{\sin(3x)}{2x}$...
Evaluate the limit:
limx→02xsin(3x)
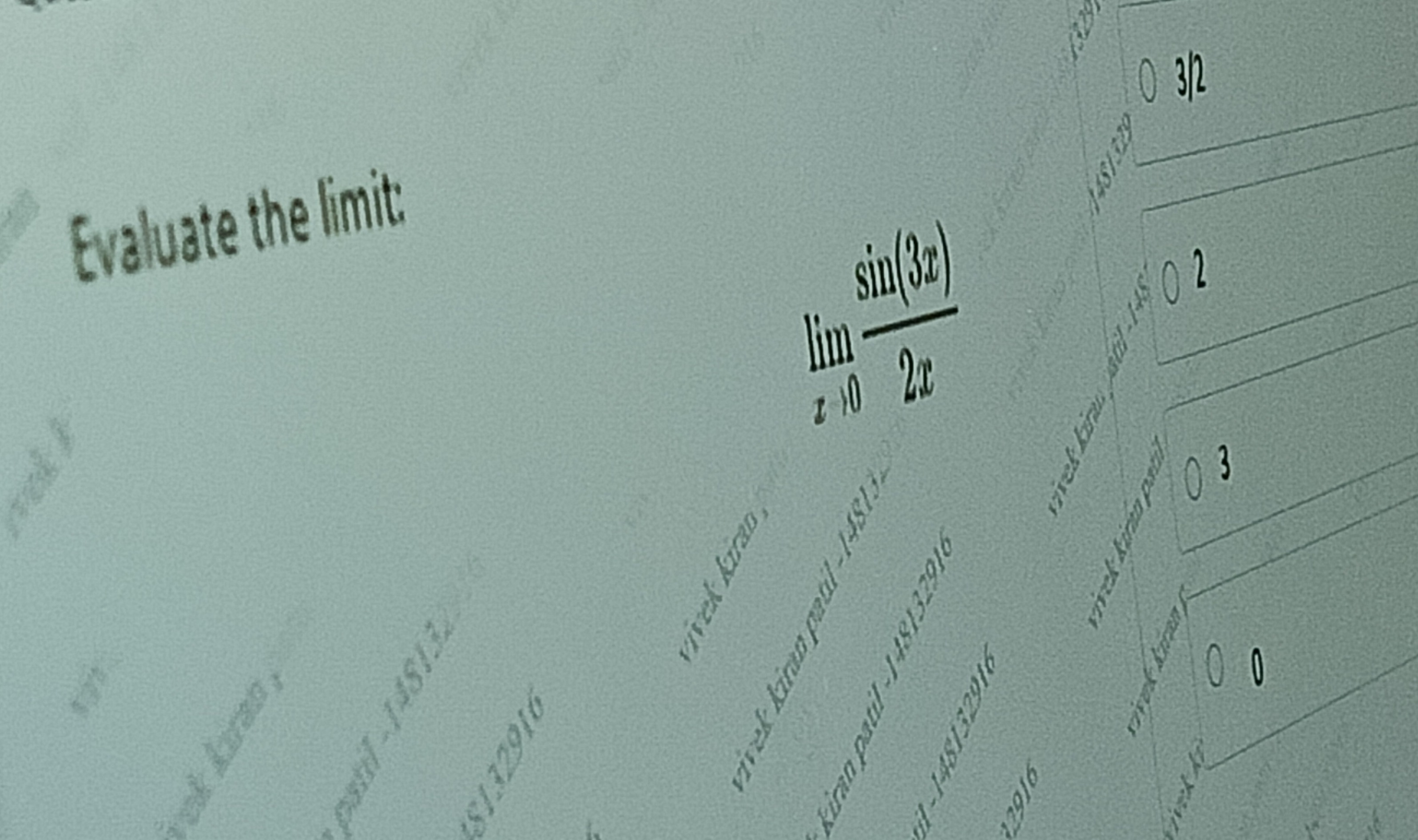
3/2
Solution
To evaluate the limit limx→02xsin(3x), we can use the fundamental trigonometric limit: limθ→0θsin(θ)=1
The given limit is: limx→02xsin(3x)
As x→0, both the numerator sin(3x) and the denominator 2x approach 0, resulting in an indeterminate form 00.
To apply the standard limit formula, we need the argument of the sine function to be present in the denominator. The argument is 3x. So, we need 3x in the denominator. We can achieve this by multiplying and dividing by 3:
limx→02xsin(3x)=limx→02xsin(3x)×33
Rearrange the terms to group 3xsin(3x): =limx→03xsin(3x)×23
Now, we can separate the limit into two parts: =(limx→03xsin(3x))×(limx→023)
For the first part, let y=3x. As x→0, y→3(0)=0. So, the first limit becomes: limy→0ysin(y)=1
The second part is a constant, so its limit is the constant itself: limx→023=23
Substitute these values back into the expression: =1×23=23
Thus, the value of the limit is 23.
