Solveeit Logo
Login

Question

Question: Evaluate the given identity \[{\sin ^{ - 1}}\left( {\dfrac{3}{5}} \right)\]?...

Evaluate the given identity sin⁡−1(35){\sin ^{ - 1}}\left( {\dfrac{3}{5}} \right)?

Explanation

Solution

Here the value given in the question with the trigonometric identity is a very well known value for which a right angle triangle is drawn in which one angle is perpendicular and rest are the sum of ninety degrees, and values of length of the sides are also known for this triangle.

Complete step by step solution:
For the given equation sin⁡−1(35){\sin ^{ - 1}}\left( {\dfrac{3}{5}} \right). We can draw the right angle triangle whose sides and angles are already known to us, let the vertex of triangle be A,B,C, now picturing the triangle with the known angles and the length of the sides, we get:

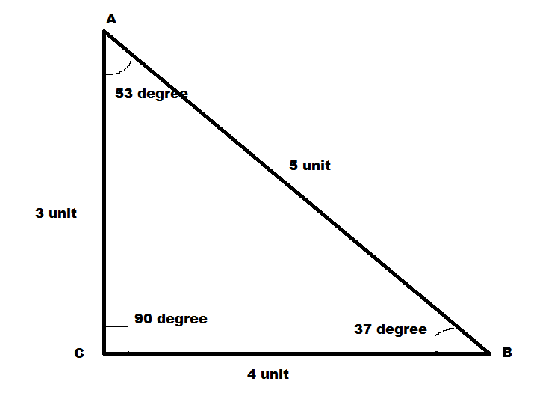
This triangle is very famous because of the values it is having with the sides of the triangle, we can see that the values are in the increment of one.In our question the angle asked for the identity with the ratio having perpendicular and base, and for “sin” identity the formula includes the ratio of perpendicular and base, so from this we can conclude that;

⇒sin - 1(35)=θ ⇒sin⁡θ=(35) ⇒θ=37o \Rightarrow {\text{si}}{{\text{n}}^{{\text{ - 1}}}}\left( {\dfrac{{\text{3}}}{{\text{5}}}} \right) = \theta \\\ \Rightarrow \sin\theta = \left( {\dfrac{{\text{3}}}{{\text{5}}}} \right) \\\ \Rightarrow \theta = 3{{\text{7}}^{\text{o}}} \\\

As we have seen from the triangle that the value of the given “sin” ratio is “37 degrees”

Note: For any such values given in the question you have to move with the triangle only or else use a calculator, no other option in lower mathematics is not there, if you try to manipulate and adjust the equation then also no value you are going to obtain from there, so you have to remember this triangle.