Solveeit Logo
Login

Question

Question: Evaluate the following: \({{\sin }^{-1}}\left( \sin 10 \right)\) ....

Evaluate the following: sin⁡−1(sin⁡10){{\sin }^{-1}}\left( \sin 10 \right) .

Explanation

Solution

Here, the angle inside the “sine” term is not in degree but in radians, so we cannot straightforwardly say that the answer is equal to 10. We will first of all define sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) function. Then, we will plot this sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) function. Once we do this, we will find out on which part of the plot does 10 radian exists and use the definition of this part to find its value. We shall proceed like this to answer our question.

Complete step-by-step answer:
We know that the range of sin⁡x\sin x is equal to the domain of sin⁡−1x{{\sin }^{-1}}x. In this problem, we will consider the base function as: sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right). Here, since the domain of sin⁡−1x{{\sin }^{-1}}x is equal to the term operated by it, that is, sin⁡x\sin x. We can say that the domain of sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) is equal to the domain of sin⁡x\sin x, which is equal to all the real numbers. Simultaneously, the range of sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) will always be equal to: [−π2,π2]\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] .
Now, we know the plot of sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) is given by:

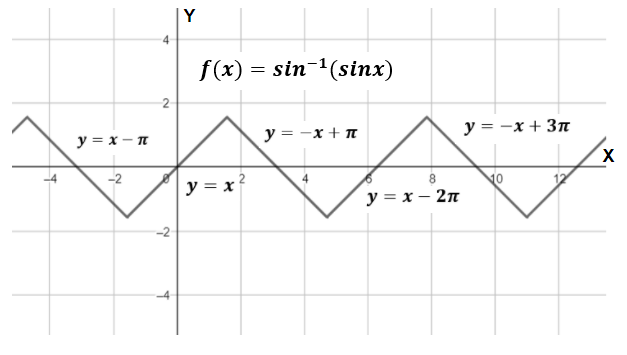
Here, we can clearly see that, for our input as 10 radian, we shall use the definition: y=−x+3πy=-x+3\pi .
Therefore, we can calculate the value of sin⁡−1(sin⁡10){{\sin }^{-1}}\left( \sin 10 \right) as follows:
⇒sin⁡−1(sin⁡10)=−10+3π ⇒sin⁡−1(sin⁡10)=−10+3×3.14 ⇒sin⁡−1(sin⁡10)=−10+9.42 ∴sin⁡−1(sin⁡10)=−0.58 \begin{aligned} & \Rightarrow {{\sin }^{-1}}\left( \sin 10 \right)=-10+3\pi \\\ & \Rightarrow {{\sin }^{-1}}\left( \sin 10 \right)=-10+3\times 3.14 \\\ & \Rightarrow {{\sin }^{-1}}\left( \sin 10 \right)=-10+9.42 \\\ & \therefore {{\sin }^{-1}}\left( \sin 10 \right)=-0.58 \\\ \end{aligned}
Hence, the value of sin⁡−1(sin⁡10){{\sin }^{-1}}\left( \sin 10 \right) comes out to be −0.58-0.58 .

Note: Whenever calculating the values of inverse of any trigonometric functions, one should always use the graphical approach. Here, we can see that, we were able to answer our question just by looking at the graph. This is the importance of remembering graphical plots of different functions be it trigonometric or non-trigonometric. These graphical plots make the understanding of mathematics easier for us.