Question

Evaluate the following
${{\operatorname{cosec}}^{3}}{{30}^{o}}\cos {{60}^{o}}{{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$

Answer 1

Hint:First of all, consider the expression given in the question. Now make the table for trigonometric ratios of general angles. Now, from that find the values of $\sin {{90}^{o}},\tan {{45}^{o}},\operatorname{cosec}{{30}^{o}},\cos {{60}^{o}},\sec {{30}^{o}}$ and $\cot {{30}^{o}}$ and substitute these in the given expression to get the required answer.

Complete step-by-step answer:
In this question, we have to find the value of the expression
${{\operatorname{cosec}}^{3}}{{30}^{o}}\cos {{60}^{o}}{{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$
Let us consider the expression given in the question.
$E={{\operatorname{cosec}}^{3}}{{30}^{o}}\cos {{60}^{o}}{{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}....\left( i \right)$
Now, we have to find the values of $\sin {{90}^{o}},\tan {{45}^{o}},\operatorname{cosec}{{30}^{o}},\cos {{60}^{o}},\sec {{30}^{o}}$ and $\cot {{30}^{o}}$.
Let us make the table for trigonometric ratios of general angles like ${{0}^{o}},{{30}^{o}},{{45}^{o}},{{60}^{o}},{{90}^{o}}$ and find the required values.

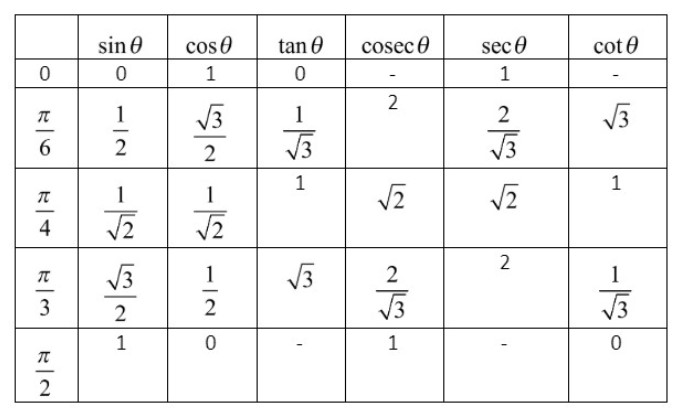
From the above table, we get, $\operatorname{cosec}{{30}^{o}}=2$. By substituting this in equation (i), we get,
$E={{\left( 2 \right)}^{3}}\cos {{60}^{o}}{{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$
Also from the above table, we get $\cos {{60}^{o}}=\dfrac{1}{2}$. By substituting this in the above equation, we get, $E={{\left( 2 \right)}^{3}}\left( \dfrac{1}{2} \right){{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$
From the table, we also get, $\tan {{45}^{o}}=1$. By substituting this in the above equation, we get,
$E={{\left( 2 \right)}^{3}}\left( \dfrac{1}{2} \right){{\left( 1 \right)}^{3}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$
From the table, we also get, $\sin {{90}^{o}}=1$. By substituting this in the above equation, we get,
$E={{\left( 2 \right)}^{3}}\left( \dfrac{1}{2} \right){{\left( 1 \right)}^{3}}{{\left( 1 \right)}^{2}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$
From the table, we also get, $\sec {{45}^{o}}=\sqrt{2}$. By substituting this in the above equation, we get,
$E={{\left( 2 \right)}^{3}}\left( \dfrac{1}{2} \right){{\left( 1 \right)}^{3}}{{\left( 1 \right)}^{2}}{{\left( \sqrt{2} \right)}^{2}}\cot {{30}^{o}}$
From the table, we also get, $\cot {{30}^{o}}=\sqrt{3}$. By substituting this in the above equation, we get,
$E={{\left( 2 \right)}^{3}}\left( \dfrac{1}{2} \right){{\left( 1 \right)}^{3}}{{\left( 1 \right)}^{2}}{{\left( \sqrt{2} \right)}^{2}}\left( \sqrt{3} \right)$
By simplifying the above equation, we get,
$E=8\times \dfrac{1}{2}\times 1\times 1\times 2\times \sqrt{3}$
$E=\dfrac{8\times 2\times \sqrt{3}}{2}$
$E=8\sqrt{3}$
Hence, we get the value of the expression ${{\operatorname{cosec}}^{3}}{{30}^{o}}\cos {{60}^{o}}{{\tan }^{3}}{{45}^{o}}{{\sin }^{2}}{{90}^{o}}{{\sec }^{2}}{{45}^{o}}\cot {{30}^{o}}$ as $8\sqrt{3}$.

Note: In these types of questions, students are advised to remember the trigonometric table for general angles. In case if they can’t remember the whole table, they just need to remember the values of $\sin \theta$ and $\cos \theta$ at various angles like ${{0}^{o}},{{30}^{o}},{{60}^{o}},{{45}^{o}},$ etc. and they can find all other trigonometric ratios using them. For example, in the above question, they can find $\operatorname{cosec}{{30}^{o}}$ by using $\dfrac{1}{\sin {{30}^{o}}},\tan {{45}^{o}}$ by $\dfrac{\sin {{45}^{o}}}{\cos {{45}^{o}}},\sec {{45}^{o}}$ by using $\dfrac{1}{\cos {{45}^{o}}}$ and $\cot {{45}^{o}}$ by using $\dfrac{\cos {{45}^{o}}}{\sin {{45}^{o}}}$.