Solveeit Logo
Login

Question

Question: Evaluate the following limit, \(\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}\) ....

Evaluate the following limit, lim⁡x→0+x1x\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} .

Explanation

Solution

First, we should take logarithms and simplify it into two decomposed limits. We may need to use the graph of ln⁡x\ln x. Then we should solve these two limits individually, and finally take exponential to get our final answer.

Complete step by step answer:
Let us assume a variable L such that,
L=lim⁡x→0+x1xL=\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}}
Let us now take logarithms on both sides of this equation. Thus, we get
ln⁡L=ln⁡(lim⁡x→0+x1x)\ln L=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)
We know that for x>0x>0, the function ln⁡x\ln x is continuous, as obvious in the figure below,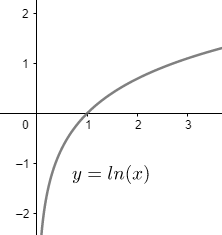
So, by the property of logarithms, we can easily write,
lim⁡x→0+(ln⁡x1x)=ln⁡(lim⁡x→0+x1x)\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right)
Using this property, we can now write,
ln⁡L=lim⁡x→0+(ln⁡x1x)...(i)\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)...\left( i \right)
We know the property of logarithms that says,
log⁡xm=mlog⁡x\log {{x}^{m}}=m\log x
So, by using this property into equation (i), we can now say that
ln⁡L=lim⁡x→0+(1xln⁡x)...(ii)\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\left( \dfrac{1}{x}\ln x \right)...\left( ii \right)
We know very well that limit is always distributive. So, we know that lim⁡x→a(ab)=lim⁡x→aa⋅lim⁡x→ab\displaystyle \lim_{x \to a}\left( ab \right)=\displaystyle \lim_{x \to a}a\cdot \displaystyle \lim_{x \to a}b
Hence, using this property of limits, we can write equation (ii) as,
ln⁡L=lim⁡x→0+1x⋅lim⁡x→0+ln⁡x...(iii)\ln L=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}\cdot \displaystyle \lim_{x \to {{0}^{+}}}\ln x...\left( iii \right)
Now, let us assume 2 variables such that, A=lim⁡x→0+1xA=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x} and B=lim⁡x→0+ln⁡xB=\displaystyle \lim_{x \to {{0}^{+}}}\ln x. So, now we can write equation (iii) as
ln⁡L=A⋅B...(iv)\ln L=A\cdot B...\left( iv \right)
Let us solve for A and B separately.
We have A=lim⁡x→0+1xA=\displaystyle \lim_{x \to {{0}^{+}}}\dfrac{1}{x}.
We know that when xx comes closer and closer to 0 from the right side, the value of A becomes larger and larger up to infinity.
Thus as xx tends to 0 or a very small positive number, the value of A tends to positive infinity.
Thus, we have A=+∞A=+\infty .
We also have B=lim⁡x→0+ln⁡xB=\displaystyle \lim_{x \to {{0}^{+}}}\ln x.
From the graph of ln⁡x\ln x , we can see that as the value of xx comes closer and closer to 0 from the right side, the value of ln⁡x\ln x becomes larger and larger but on the negative side.
Thus, we can say that as xx tends to 0 or very small positive numbers, the value of B tends to negative infinity.
Thus, we have B=−∞B=-\infty .
Putting the values of A and B into equation (iv), we get
ln⁡L=(∞)⋅(−∞)\ln L=\left( \infty \right)\cdot \left( -\infty \right)
⇒ln⁡L=−∞\Rightarrow \ln L=-\infty
Now, taking exponentials on both sides of the equation, we get
eln⁡L=e−∞{{e}^{\ln L}}={{e}^{-\infty }}
⇒L=0\Rightarrow L=0
Thus, the value of lim⁡x→0+x1x\displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} is 0.

Note: We must always verify whether the function is continuous or not before applying lim⁡x→0+(ln⁡x1x)=ln⁡(lim⁡x→0+x1x)\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln {{x}^{\dfrac{1}{x}}} \right)=\ln \left( \displaystyle \lim_{x \to {{0}^{+}}}{{x}^{\dfrac{1}{x}}} \right). We must remember that any number raised to negative infinity is 0. And so, the term e−∞{{e}^{-\infty }} is equal to 0.