Question

Evaluate the following expression- $\sin {{0}^{c}}+2\cos {{0}^{c}}+3\sin {{\left( \dfrac{\pi }{2} \right)}^{c}}+4\cos {{\left( \dfrac{\pi }{2} \right)}^{c}}+5\sec {{0}^{c}}+6\text{cosec}{{\left( \dfrac{\pi }{2} \right)}^{c}}$ .

Answer 1

Hint: The given angles are in radians and we can convert them into degrees. Then, we can see that all the angles are standard angles. We can simplify it by converting sec in terms of cos and cosec in terms of sin and then just put the respective values.

Complete step-by-step answer:
The expression given in the question is $\sin {{0}^{c}}+2\cos {{0}^{c}}+3\sin {{\left( \dfrac{\pi }{2} \right)}^{c}}+4\cos {{\left( \dfrac{\pi }{2} \right)}^{c}}+5\sec {{0}^{c}}+6\text{cosec}{{\left( \dfrac{\pi }{2} \right)}^{c}}$.

We can convert the angle $\dfrac{\pi }{2}$ into degrees by multiplying it with $\dfrac{180}{\pi }$ . Therefore, we get that angle ${{0}^{c}}\Rightarrow 0\times \dfrac{180}{\pi }\Rightarrow 0$ and angle ${{\left( \dfrac{\pi }{2} \right)}^{c}}\Rightarrow \dfrac{\pi }{2}\times \dfrac{180}{\pi }=90{}^\circ$ . Now, we can write the given expression as,
$\text{sin}{{0}^{\circ }}+2\cos {{\text{0}}^{\circ }}+3\sin {{90}^{\circ }}+4\cos {{90}^{\circ }}+5\sec {{0}^{\circ }}+6\,\text{cosec}{{90}^{\circ }}....(1)$

The values of standard angles in degrees are given in the table below.

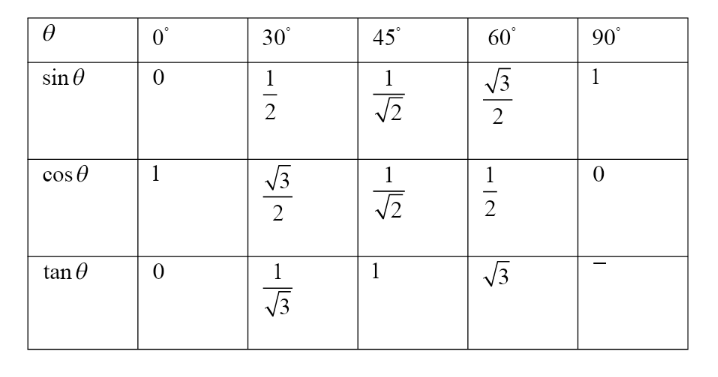
We should also remember that $\text{cosec}\,\text{x=}\dfrac{\text{1}}{\text{sin x}}$ and $\sec \,\text{x=}\dfrac{\text{1}}{\text{cos x}}$.
So now simplifying equation (1) by transforming cosec in terms of sin and sec in terms of cos, we get
$\Rightarrow \text{sin}{{0}^{\circ }}+2\cos {{\text{0}}^{\circ }}+3\sin {{90}^{\circ }}+4\cos {{90}^{\circ }}+\dfrac{5}{\cos {{0}^{\circ }}}+\dfrac{6}{\sin {{90}^{\circ }}}$

Now putting values from the above table,
$\text{= 0}+2\times 1+3\times 1+4\times 0+\dfrac{5}{1}+\dfrac{6}{1}$

Now adding all the numbers we get,
$\text{=16}$

Hence 16 is the answer.

Note: Remembering all the values of sin, cos, tan is the key here and knowing the relationship between sin and cosec, sec and cos is important. We can commit mistake in a hurry by substituting $\cos {{0}^{\circ }}=0$ instead of $\cos {{0}^{\circ }}=1$ and substituting $\sin {{90}^{\circ }}=0$ instead of $\sin {{90}^{\circ }}=1$.