Question

Evaluate the following
$4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$

Answer 1

Hint:First of all, consider the expression given in the question. Now make the table for trigonometric ratios of general angles. Now, from that find the values of $\sin {{60}^{o}},\cos {{30}^{o}},\tan {{60}^{o}},\tan {{45}^{o}}$ and $\cos {{45}^{o}}$ and substitute these in the given expression to get the required answer.

Complete step-by-step answer:
In this question, we have to find the value of the expression
$4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$
Let us consider the expression given in the question.
$E=4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}....\left( i \right)$
Now, we have to find the values of $\sin {{60}^{o}},\cos {{30}^{o}},\tan {{60}^{o}},\tan {{45}^{o}}$ and $\cos {{45}^{o}}$.
Let us make the table for trigonometric ratios of general angles like ${{0}^{o}},{{30}^{o}},{{45}^{o}},{{60}^{o}},{{90}^{o}}$ and find the required values.

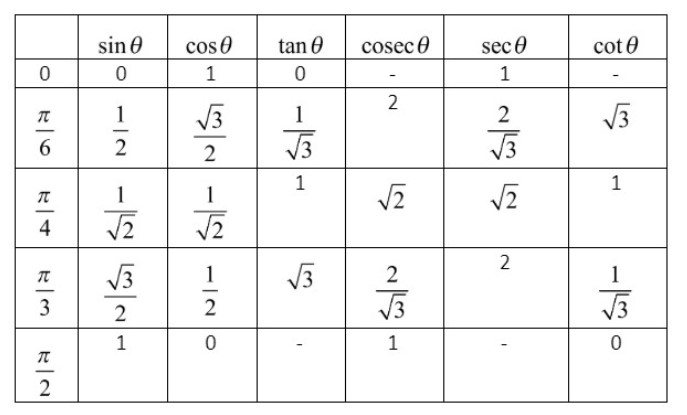
From the above table, we get, $\sin {{60}^{o}}=\dfrac{\sqrt{3}}{2}$. By substituting this in equation (i), we get,
$E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$
Also from the above table, we get $\cos {{30}^{o}}=\dfrac{\sqrt{3}}{2}$. By substituting this in the above equation, we get, $E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$
From the table, we also get, $\tan {{60}^{o}}=\sqrt{3}$. By substituting this in the above equation, we get,
$E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$
From the table, we also get, $\tan {{45}^{o}}=1$. By substituting this in the above equation, we get,
$E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}} \right)+5{{\cos }^{2}}{{45}^{o}}$
From the table, we also get, $\cos {{45}^{o}}=\dfrac{1}{\sqrt{2}}$. By substituting this in the above equation, we get,
$E=4\left( {{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{4}} \right)-3\left( {{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}} \right)+5{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}$
By simplifying the above equation, we get,
$E=4\left( \dfrac{9}{16}+\dfrac{9}{16} \right)-3\left( 3-1 \right)+5\left( \dfrac{1}{2} \right)$
$E=4\left( \dfrac{18}{16} \right)-3\left( 2 \right)+\dfrac{5}{2}$
$E=\dfrac{18}{4}-6+\dfrac{5}{2}$
$E=\dfrac{9}{2}+\dfrac{5}{2}-6$
$E=\dfrac{14}{2}-6$
$E=7-6$
$E=1$
Hence, we get the value of the expression $4\left( {{\sin }^{4}}{{60}^{o}}+{{\cos }^{4}}{{30}^{o}} \right)-3\left( {{\tan }^{2}}{{60}^{o}}-{{\tan }^{2}}{{45}^{o}} \right)+5{{\cos }^{2}}{{45}^{o}}$ as 1.

Note: In these types of questions, students just need to remember the values of $\sin \theta$ and $\cos \theta$ at various angles like ${{0}^{o}},{{30}^{o}},{{60}^{o}},{{45}^{o}},$ etc. and they can find $\tan \theta$ by using $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$. Also, students must take care of substituting the corresponding angle. For example, if we have to find $\tan {{60}^{o}}$, then we will use $\sin {{60}^{o}}$ and $\cos {{60}^{o}}$ while we have to find $\tan {{45}^{o}}$, then we will use $\sin {{45}^{o}}$ and $\cos {{45}^{o}}$ and likewise. Also, it would also be better to memorize the trigonometric table.