Question

Evaluate the definite integral:
$\int\limits_0^{\dfrac{\pi }{2}} {\cos xdx}$

Answer 1

We know that $\int {\cos xdx}$ $= \sin x$ and while putting upper and lower limits, you will get your answer.

Complete step-by-step answer:
We know that integration represents the area under the curve, here we are given to find the integral of the curve $\cos x$ in the limit from $0$ to $\dfrac{\pi }{2}$.
So now let us see by the graph what we need to find.

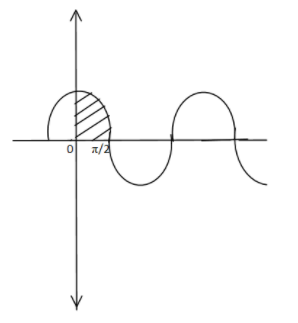
So this is the graph of $\cos x$ and we need to find the $\int\limits_0^{\dfrac{\pi }{2}} {\cos x dx}$ that means that we need to find the area which is shaded or the curve of the $\cos x$ from $0$ to $\dfrac{\pi }{2}$
Now we know that integration of $\cos x$ gives $\sin x$ and we know the formula that
$\int\limits_a^b {\cos nx} = \left[ {\dfrac{{\sin x}}{n}} \right]_a^b$
$\int\limits_a^b {\cos nx} = \left[ {\dfrac{{\sin nb}}{n} - \dfrac{{\sin na}}{n}} \right]$
So in this question, we are given:
$\int\limits_0^{\dfrac{\pi }{2}} {\cos x dx}$
Now we know that
$\int {\cos nxdx} = \left[ {\dfrac{{\sin nx}}{n}} \right]$ and here $n = 1$
So we get $\int\limits_0^{\dfrac{\pi }{2}} {\cos x} = \left[ {\sin x} \right]_0^{\dfrac{\pi }{2}}$
Here$\dfrac{\pi }{2}$ is the upper limit and $0$ is the lower limit.
So upon putting we get
$\int\limits_0^{\dfrac{\pi }{2}} {\cos x} = \left[ {\sin \dfrac{\pi }{2} - \sin 0} \right]$
We know that $\sin 0 = 0,\sin 90 = 1$
We get that
$\int\limits_0^{\dfrac{\pi }{2}} {\cos x} = \left[ {\sin \dfrac{\pi }{2} - \sin 0} \right] = 1$

Note: We should know that if $\dfrac{{df(x)}}{{dx}} = g(x)$, then $\int {g(x)dx}$ gives $f(x)$ or vice-versa similarly.
$\int {\cos x} dx$ gives $\sin x$. So $\dfrac{{d\sin x}} {{dx}} = \cos x$