Solveeit Logo
Login

Question

Question: Evaluate \[\tan \left( {{{\sec }^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)} \right)\]. (A) \( \df...

Evaluate tan⁡(sec⁡−1(1+x2))\tan \left( {{{\sec }^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)} \right).
(A) 1x\dfrac{1}{x}
(B) xx
(C) 11+x2\dfrac{1}{{\sqrt {1 + {x^2}} }}
(D) x1+x2\dfrac{x}{{\sqrt {1 + {x^2}} }}

Explanation

Solution

Hint : In the given problem, we are required to calculate the tangent of an angle whose secant is given to us. Such problems require basic knowledge of trigonometric ratios and formulae. Besides this, knowledge of concepts of inverse trigonometry is extremely essential to answer these questions correctly. We must know the principal value branches of all the inverse trigonometric functions.

Complete step-by-step answer :
So, In the given problem, we have to find the value of tan⁡(sec⁡−1(1+x2))\tan \left( {{{\sec }^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)} \right).
Hence, we have to find the tangent of the angle whose secant is given to us as tan⁡(sec⁡−1(1+x2))\tan \left( {{{\sec }^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)} \right).
Let us assume θ\theta to be the concerned angle.
Then, θ=sec⁡−1(1+x2)\theta = {\sec ^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)
Taking secant on both sides of the equation, we get
⇒sec⁡θ=1+x2\Rightarrow \sec \theta = \sqrt {1 + {x^2}}
To evaluate the value of the required expression, we must keep in mind the formulae of basic trigonometric ratios.
We know that, tan⁡θ=PerpendicularBase\tan \theta = \dfrac{{Perpendicular}}{{Base}} and sec⁡θ=HypotenuseBase\sec \theta = \dfrac{{Hypotenuse}}{{Base}} .
So, sec⁡θ=HypotenuseBase=1+x2\sec \theta = \dfrac{{Hypotenuse}}{{Base}} = \sqrt {1 + {x^2}}
Let the length of the base be 11 .
Then, length of hypotenuse =1+x2= \sqrt {1 + {x^2}} .

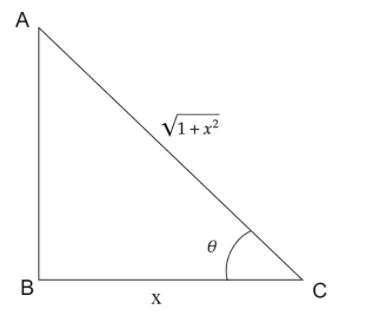
Now, applying Pythagoras Theorem,
(Hypotenuse)2=(Base)2+(Perpendicular)2{\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Perpendicular} \right)^2}
⇒(1+x2)2=(1)2+(Perpendicular)2\Rightarrow {\left( {\sqrt {1 + {x^2}} } \right)^2} = {\left( 1 \right)^2} + {\left( {Perpendicular} \right)^2}
⇒1+x2=1+(Perpendicular)2\Rightarrow 1 + {x^2} = 1 + {\left( {Perpendicular} \right)^2}
Subtracting one from both the sides of the equation. So, we get,
⇒x2=(Perpendicular)2\Rightarrow {x^2} = {\left( {Perpendicular} \right)^2}
⇒(Perpendicular)=x\Rightarrow \left( {Perpendicular} \right) = x
So, we get, (Perpendicular)=x\left( {Perpendicular} \right) = x
Hence, tan⁡θ=PerpendicularBase=x1+x2\tan \theta = \dfrac{{Perpendicular}}{{Base}} = \dfrac{x}{{\sqrt {1 + {x^2}} }}
So, the value oftan⁡(sec⁡−1(1+x2))\tan \left( {{{\sec }^{ - 1}}\left( {\sqrt {1 + {x^2}} } \right)} \right) is x1+x2\dfrac{x}{{\sqrt {1 + {x^2}} }} .
So, the correct answer is option (D).
So, the correct answer is “Option D”.

Note : The given problem can also be solved by use of some basic trigonometric identities such as sec⁡2(θ)=tan⁡2(θ)+1{\sec ^2}\left( \theta \right) = {\tan ^2}\left( \theta \right) + 1 .
We have, sec⁡θ=1+x2\sec \theta = \sqrt {1 + {x^2}}
So, sec⁡2θ=1+x2{\sec ^2}\theta = 1 + {x^2}
Using sec⁡2(θ)=tan⁡2(θ)+1{\sec ^2}\left( \theta \right) = {\tan ^2}\left( \theta \right) + 1 , we get,
⇒tan⁡2θ+1=1+x2\Rightarrow {\tan ^2}\theta + 1 = 1 + {x^2}
Finding value of tangent function,
⇒tan⁡2θ=x2\Rightarrow {\tan ^2}\theta = {x^2}
Taking square root on both sides,
⇒tan⁡θ=x\Rightarrow \tan \theta = x
This method also provides exposure to the applications of trigonometric identities in various mathematical questions. We should remember all the trigonometric formulae and identities in order to solve such questions. One should know about the principal branches of all the inverse trigonometric functions. Care should be taken while doing the calculations so as to be sure of the final answer.