Solveeit Logo
Login

Question

Question: Evaluate \[{\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right)\] A. \[\d...

Evaluate tan⁡−1(3)−sec⁡−1(−2){\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right)
A. π3\dfrac{\pi }{3}
B. −π3 - \dfrac{\pi }{3}
C. 5π3\dfrac{{5\pi }}{3}
D. None of these

Explanation

Solution

Here we write the values of numbers in the bracket as trigonometric functions of the respective inverse. Use the trigonometric table that gives the values at some common angles to write the values. Use the quadrant diagram to find the value of the negative term inside the bracket.

Complete step-by-step answer:
We have to find the value of tan⁡−1(3)−sec⁡−1(−2){\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right).............… (1)
We know from the trigonometric table tan⁡60∘=3\tan {60^ \circ } = \sqrt 3
⇒tan⁡π3=3\Rightarrow \tan \dfrac{\pi }{3} = \sqrt 3 ………...… (2)
Now we know sec⁡60∘=2\sec {60^ \circ } = 2
⇒sec⁡π3=2\Rightarrow \sec \dfrac{\pi }{3} = 2
Use the quadrant diagram to convert the value from 2 to -2 by adding or subtracting the angle.
We have quadrant diagram as

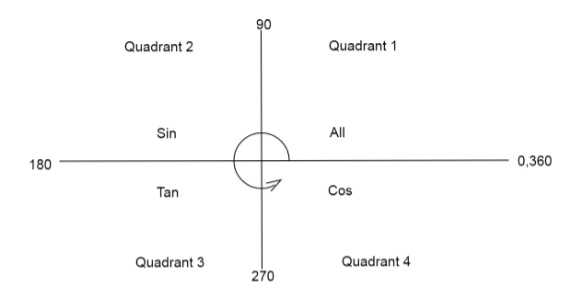
Since ‘cos’ is negative in the second and third quadrant, we add or subtract angle accordingly.
We have sec⁡π3=2\sec \dfrac{\pi }{3} = 2
If we subtract the given angle from π\pi , the value of the function will become negative.
We can write sec⁡(π−π3)=−2\sec (\pi - \dfrac{\pi }{3}) = - 2 ………...… (3)
Substitute the values from equation (2) and (3) back in equation (1)
⇒tan⁡−1(3)−sec⁡−1(−2)=tan⁡−1(tan⁡π3)−sec⁡−1(sec⁡(π−π3))\Rightarrow {\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) = {\tan ^{ - 1}}\left({\tan \dfrac{\pi }{3}} \right) - {\sec ^{ - 1}}\left( {\sec \left( {\pi - \dfrac{\pi }{3}} \right)} \right)
Since we know f−1(f(x))=x{f^{ - 1}}(f(x)) = x
⇒tan⁡−1(3)−sec⁡−1(−2)=(π3)−(π−π3)\Rightarrow {\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) = \left( {\dfrac{\pi}{3}} \right) - \left( {\pi - \dfrac{\pi }{3}} \right)
Solve the RHS of the equation by opening the brackets
⇒tan⁡−1(3)−sec⁡−1(−2)=π3−π+π3\Rightarrow {\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) = \dfrac{\pi }{3} - \pi+ \dfrac{\pi }{3}
Take LCM in RHS of the equation
⇒tan⁡−1(3)−sec⁡−1(−2)=π−3π+π3\Rightarrow {\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) = \dfrac{{\pi - 3\pi +\pi }}{3}
Calculate the numerator in RHS of the equation
⇒tan⁡−1(3)−sec⁡−1(−2)=−π3\Rightarrow {\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) = \dfrac{{ - \pi }}{3}
∴\therefore The value of tan⁡−1(3)−sec⁡−1(−2){\tan ^{ - 1}}\left( {\sqrt 3 } \right) - {\sec ^{ - 1}}\left( { - 2} \right) is −π3\dfrac{{ - \pi }}{3}.

∴\therefore Option B is correct.

Note: Inverse of any function when applied on the same function cancels out the function and the inverse, i.e. f−1(f(x))=x{f^{ - 1}}(f(x)) = x.
Students many times get confused while adding and subtracting angles to change the sign
from negative to positive and vice versa. Keep in mind we move to that quadrant where the
trigonometric function has the required sign.