Question
Question: Evaluate \[ \sum_{k=1}^{100} \frac{1\cdot4}{2}+\frac{1\cdot4\cdot7}{2\cdot5}+\frac{1\cdot4\cdot7\cdo...
Evaluate
k=1∑10021⋅4+2⋅51⋅4⋅7+2⋅5⋅81⋅4⋅7⋅10+…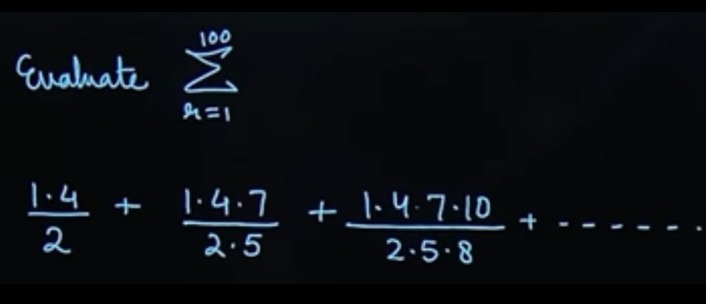
Answer
21(2⋅5⋅8⋅…⋅2991⋅4⋅7⋅…⋅301−3)
Explanation
Solution
Let Tk=2⋅5⋅8⋅⋯⋅(3k−1)1⋅4⋅7⋅⋯⋅(3k−2). We want to evaluate ∑k=1100Tk. The general term is Tk=2⋅5⋅8⋅⋯⋅(3k−1)1⋅4⋅7⋅⋯⋅(3k−2).
The sum of n terms is given by the formula:
Sn=21(2⋅5⋅8⋅…⋅(3n−1)1⋅4⋅7⋅…⋅(3n−2)⋅(3n+1)−3).
Substituting n=100:
∑k=1100Tk=21(2⋅5⋅8⋅…⋅(3⋅100−1)1⋅4⋅7⋅…⋅(3⋅100−2)⋅(3⋅100+1)−3)
∑k=1100Tk=21(2⋅5⋅8⋅…⋅2991⋅4⋅7⋅…⋅298⋅301−3).
Therefore, the final answer is 21(2⋅5⋅8⋅…⋅2991⋅4⋅7⋅…⋅301−3).
