Question

Evaluate: $\log_3 4 . \log_4 5 . \log_5 6 . \log_6 7 . \log_7 8 . \log_8 9$

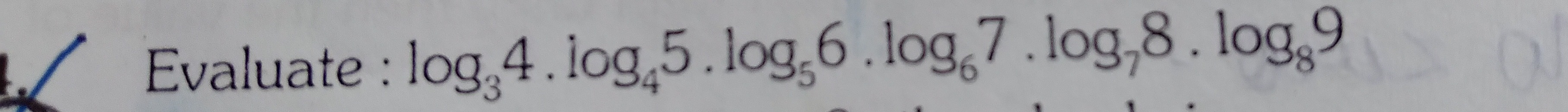
Answer 1

2

Answer 2

To evaluate the given expression, we use the change of base formula for logarithms, which states that $\log_b a = \frac{\log_c a}{\log_c b}$. Using the natural logarithm (ln) as the base: $\log_3 4 \cdot \log_4 5 \cdot \log_5 6 \cdot \log_6 7 \cdot \log_7 8 \cdot \log_8 9$ Applying the change of base formula to each term: $\left(\frac{\ln 4}{\ln 3}\right) \cdot \left(\frac{\ln 5}{\ln 4}\right) \cdot \left(\frac{\ln 6}{\ln 5}\right) \cdot \left(\frac{\ln 7}{\ln 6}\right) \cdot \left(\frac{\ln 8}{\ln 7}\right) \cdot \left(\frac{\ln 9}{\ln 8}\right)$ This results in a telescoping product where intermediate terms cancel out: $\frac{\cancel{\ln 4}}{\cancel{\ln 3}} \cdot \frac{\cancel{\ln 5}}{\cancel{\ln 4}} \cdot \frac{\cancel{\ln 6}}{\cancel{\ln 5}} \cdot \frac{\cancel{\ln 7}}{\cancel{\ln 6}} \cdot \frac{\cancel{\ln 8}}{\cancel{\ln 7}} \cdot \frac{\ln 9}{\cancel{\ln 8}} = \frac{\ln 9}{\ln 3}$ Using the change of base formula in reverse or evaluating directly: $\frac{\ln 9}{\ln 3} = \log_3 9$ Since $9 = 3^2$: $\log_3 9 = \log_3 (3^2)$ Using the logarithm property $\log_b (b^x) = x$: $\log_3 (3^2) = 2$ Thus, the value of the expression is $2$.