Solveeit Logo
Login

Question

Question: Evaluate: $\lim_{x\to 0} \frac{\sin(3x) - 3\sin(x)}{x^3}$...

Evaluate:

lim⁡x→0sin⁡(3x)−3sin⁡(x)x3\lim_{x\to 0} \frac{\sin(3x) - 3\sin(x)}{x^3}

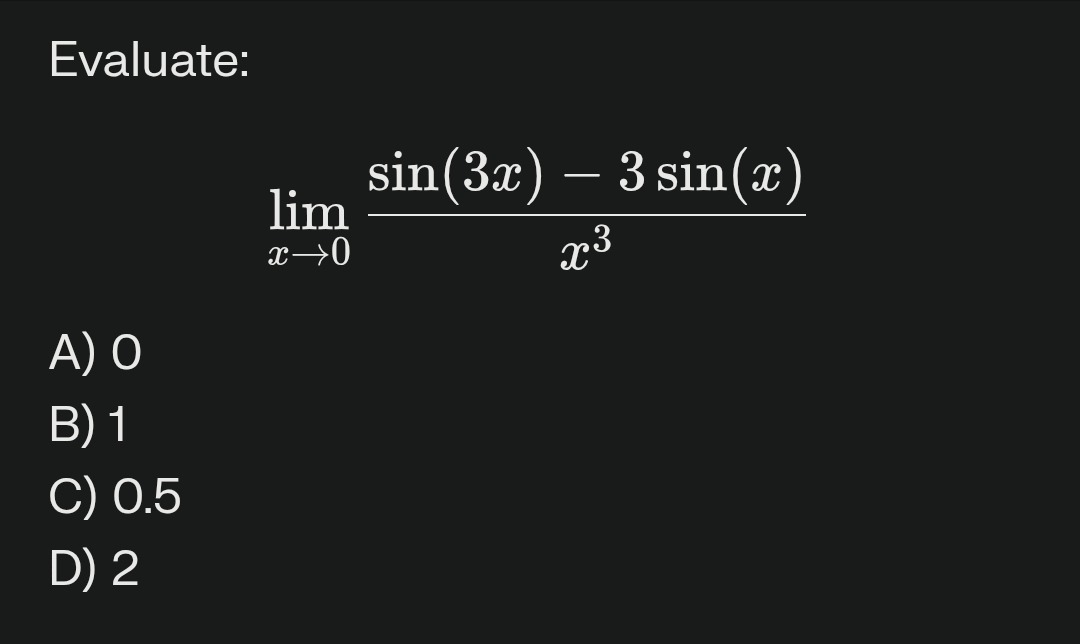
A

0

B

1

C

0.5

D

2

Answer

-4

Explanation

Solution

We can evaluate the limit using the trigonometric identity sin⁡(3x)=3sin⁡(x)−4sin⁡3(x)\sin(3x) = 3\sin(x) - 4\sin^3(x). Substituting this into the expression gives:

sin⁡(3x)−3sin⁡(x)x3=(3sin⁡(x)−4sin⁡3(x))−3sin⁡(x)x3=−4sin⁡3(x)x3\frac{\sin(3x) - 3\sin(x)}{x^3} = \frac{(3\sin(x) - 4\sin^3(x)) - 3\sin(x)}{x^3} = \frac{-4\sin^3(x)}{x^3}.

This can be rewritten as −4(sin⁡(x)x)3-4 \left(\frac{\sin(x)}{x}\right)^3.

Applying the limit lim⁡x→0sin⁡(x)x=1\lim_{x\to 0} \frac{\sin(x)}{x} = 1, we get:

−4(1)3=−4-4(1)^3 = -4.

Therefore, the limit evaluates to -4.