Question
Question: Evaluate: $ \lim_{x \to \infty} \frac{\log 4 + \log (0.5+x)}{\sqrt{x}}$...
Evaluate: limx→∞xlog4+log(0.5+x)
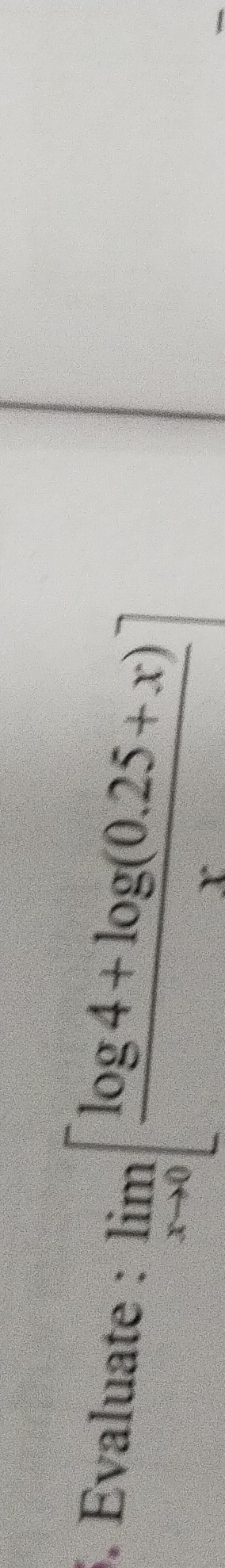
0
Solution
To evaluate the limit limx→∞xlog4+log(0.5+x), we follow these steps:
-
Simplify the numerator: Using the logarithm property logA+logB=log(AB), we can combine the terms in the numerator: log4+log(0.5+x)=log(4⋅(0.5+x))=log(2+4x) So the limit becomes: limx→∞xlog(2+4x)
-
Check the indeterminate form: As x→∞: Numerator: log(2+4x)→∞ (since 2+4x→∞) Denominator: x→∞ The limit is of the indeterminate form ∞∞, so we can apply L'Hôpital's Rule.
-
Apply L'Hôpital's Rule (First time): Let f(x)=log(2+4x) and g(x)=x. Find their derivatives: f′(x)=dxd(log(2+4x))=2+4x1⋅dxd(2+4x)=2+4x4 g′(x)=dxd(x)=dxd(x1/2)=21x−1/2=2x1 Now, apply L'Hôpital's Rule: limx→∞g′(x)f′(x)=limx→∞2x12+4x4 =limx→∞2+4x4⋅2x =limx→∞2+4x8x
-
Evaluate the new limit: The new limit is still of the form ∞∞. We can either apply L'Hôpital's Rule again or simplify by dividing the numerator and denominator by the highest power of x in the denominator, which is x. Dividing numerator and denominator by x: =limx→∞x2+x4xx8x =limx→∞x2+4x8 Now, evaluate the terms as x→∞: As x→∞, x8→0. As x→∞, x2→0. So the limit becomes: 0+40=40=0
