Solveeit Logo
Login

Question

Question: Evaluate \(\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos ...

Evaluate (cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)

Explanation

Solution

Hint:The Trigonometric ratios table helps to find the values of trigonometric standard angles such as 00,300,450,600{{0}^{0}},{{30}^{0}},{{45}^{0}},{{60}^{0}} and 900{{90}^{0}}. It consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant and cotangent. These ratios can be written in short as sin, cos, tan, cosec, sec and cot.

Complete step-by-step answer:
The calculus is based on trigonometry and algebra. The fundamental trigonometric functions like sine and cosine are used to describe the sound and light waves. Trigonometry is used in oceanography to calculate heights of waves and tides in oceans. It is used in satellite systems.
Let us make the table for trigonometric ratios of general angles

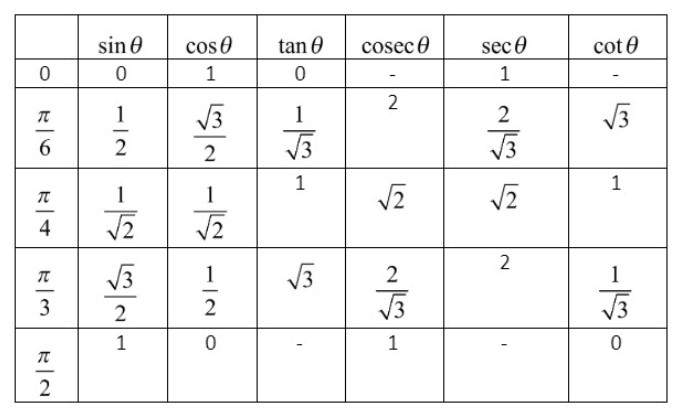
The value of the trigonometric ratios by using the trigonometric table is given below.
cos⁡00=1,sin⁡300=12,sin⁡450=12,sin⁡900=1,cos⁡600=12,cos⁡450=12\cos {{0}^{0}}=1,\sin {{30}^{0}}=\dfrac{1}{2},\sin {{45}^{0}}=\dfrac{1}{\sqrt{2}},\sin {{90}^{0}}=1,\cos {{60}^{0}}=\dfrac{1}{2},\cos {{45}^{0}}=\dfrac{1}{\sqrt{2}}
Let us consider the given expression and put all the trigonometric values, we get
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=(1+12+12)(1−12+12)\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\left( 1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{2} \right)\left( 1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{2} \right)
Rearranging the terms on right side, we get
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=(32+12)(32−12)\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\left( \dfrac{3}{2}+\dfrac{1}{\sqrt{2}} \right)\left( \dfrac{3}{2}-\dfrac{1}{\sqrt{2}} \right)
Applying the algebraic identity (a+b)(a−b)=a2−b2\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}} on the right side, we get
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=(32)2−(12)2\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)={{\left( \dfrac{3}{2} \right)}^{2}}-{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=94−12\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\dfrac{9}{4}-\dfrac{1}{2}
Taking the LCM on the right side, we get
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=18−48\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\dfrac{18-4}{8}
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=148\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\dfrac{14}{8}
(cos⁡00+sin⁡450+sin⁡300)(sin⁡900−cos⁡450+cos⁡600)=74\left( \cos {{0}^{0}}+\sin {{45}^{0}}+\sin {{30}^{0}} \right)\left( \sin {{90}^{0}}-\cos {{45}^{0}}+\cos {{60}^{0}} \right)=\dfrac{7}{4}
Hence the required value of the given expression is 74\dfrac{7}{4}.

Note: In these types of questions, students must take care of the calculation that should be done according to the BODMAS rule. Also, students are advised to memorize at least the values of sin⁡θ\sin \theta and cos⁡θ\cos \theta at different angles and from these values, they can find all the other trigonometric ratios.SOHCAHTOA, A way of remembering how to compute the sine, cosine, and tangent of an angle. SOH stands for Sine equals Opposite over Hypotenuse. CAH stands for Cosine equals Adjacent over Hypotenuse. TOA stands for Tangent equals Opposite over Adjacent.