Question

\int_{1}^{4} (|x| + |3-x|) , dx

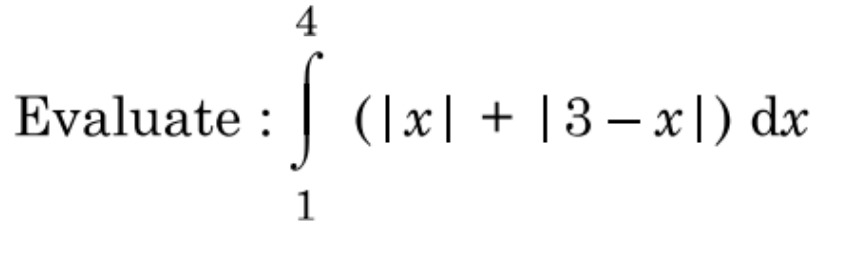
Answer 1

10

Answer 2

The integral is split at $x=3$: For $x \in [1, 3]$, $|x| = x$ and $|3-x| = 3-x$. The integrand is $x + (3-x) = 3$. For $x \in [3, 4]$, $|x| = x$ and $|3-x| = -(3-x) = x-3$. The integrand is $x + (x-3) = 2x-3$.

The integral becomes: $\int_{1}^{3} 3 \, dx + \int_{3}^{4} (2x-3) \, dx$ $= [3x]_{1}^{3} + [x^2 - 3x]_{3}^{4}$ $= (9 - 3) + ((16 - 12) - (9 - 9))$ $= 6 + (4 - 0) = 6 + 4 = 10$