Question

Evaluate : $\int_{0}^{\frac{\pi}{4}} \frac{dx}{\cos^3 x\sqrt{2 \sin 2x}}.$

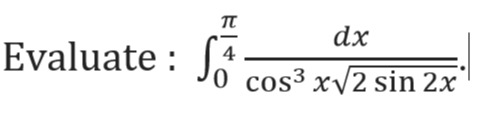
Answer 1

1

Answer 2

1. Simplify $\sqrt{2 \sin 2x} = \sqrt{4 \sin x \cos x} = 2\sqrt{\sin x \cos x}$.
2. Manipulate the integrand: $\frac{1}{\cos^3 x \cdot 2\sqrt{\sin x \cos x}} = \frac{\sec^4 x}{2\sqrt{\tan x}}$.
3. Substitute $u = \tan x$, so $du = \sec^2 x dx$. The limits change from $0, \frac{\pi}{4}$ to $0, 1$.
4. The integral becomes $\frac{1}{2} \int_{0}^{1} u^{-1/2} du$.
5. Evaluate: $\frac{1}{2} [2\sqrt{u}]_{0}^{1} = [\sqrt{u}]_{0}^{1} = \sqrt{1} - \sqrt{0} = 1$.