Question

Evaluate: $\int_{0}^{1} \frac{log(1+x)}{1+x^2} dx$

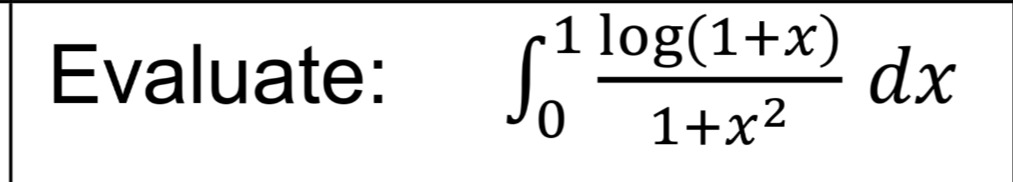
Answer 1

$\frac{\pi}{8} \log 2$

Answer 2

Let the integral be $I$. Using the substitution $x = \tan \theta$, we get $I = \int_{0}^{\pi/4} \log(1+\tan \theta) d\theta$. Applying the property $\int_{0}^{a} f(x) dx = \int_{0}^{a} f(a-x) dx$, we get $I = \int_{0}^{\pi/4} \log\left(1+\tan\left(\frac{\pi}{4}-\theta\right)\right) d\theta$. Using the tangent subtraction formula, this simplifies to $I = \int_{0}^{\pi/4} (\log 2 - \log(1+\tan \theta)) d\theta$. This leads to $I = \frac{\pi}{4} \log 2 - I$. Solving for $I$ gives $I = \frac{\pi}{8} \log 2$.