Question
Question: Evaluate $\int (\sqrt{25-9x^2})dx$....
Evaluate ∫(25−9x2)dx.
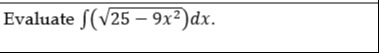
2x25−9x2+625sin−1(53x)+C
Solution
The integral to evaluate is ∫(25−9x2)dx.
Explanation of the solution:
-
Rewrite the integrand: The expression inside the square root can be written as 52−(3x)2. So, the integral is ∫52−(3x)2dx.
-
Substitution: Let u=3x. Differentiating both sides with respect to x, we get du=3dx. This implies dx=31du.
-
Transform the integral: Substitute u and dx into the integral: ∫52−u2(31du)=31∫52−u2du
-
Apply standard integral formula: The integral is now in the standard form ∫a2−x2dx, where a=5 and the variable is u. The formula for this integral is: ∫a2−x2dx=2xa2−x2+2a2sin−1(ax)+C Applying this formula with a=5 and variable u: 31[2u52−u2+252sin−1(5u)]+C
-
Substitute back: Replace u with 3x: 31[23x25−(3x)2+225sin−1(53x)]+C
-
Simplify: 31[23x25−9x2+225sin−1(53x)]+C =63x25−9x2+625sin−1(53x)+C =2x25−9x2+625sin−1(53x)+C
