Solveeit Logo
Login

Question

Question: Evaluate: $\int \frac{x^2-x^3}{(x+1)(x^3+x^2+x)^{3/2}} dx$...

Evaluate: ∫x2−x3(x+1)(x3+x2+x)3/2dx\int \frac{x^2-x^3}{(x+1)(x^3+x^2+x)^{3/2}} dx

Answer

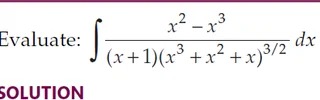
2\left(\frac{\sqrt{x}}{\sqrt{x^2+x+1}} - \arccos\left(\frac{\sqrt{x^2+x+1}}{x+1}\right)\right) + C

Explanation

Solution

To evaluate the integral I=∫x2−x3(x+1)(x3+x2+x)3/2dxI = \int \frac{x^2-x^3}{(x+1)(x^3+x^2+x)^{3/2}} dx, we follow these steps:

  1. Simplify the integrand: The term x3+x2+xx^3+x^2+x can be factored as x(x2+x+1)x(x^2+x+1). So the integral becomes: I=∫x2−x3(x+1)(x(x2+x+1))3/2dxI = \int \frac{x^2-x^3}{(x+1)(x(x^2+x+1))^{3/2}} dx I=∫x2(1−x)(x+1)x3/2(x2+x+1)3/2dxI = \int \frac{x^2(1-x)}{(x+1)x^{3/2}(x^2+x+1)^{3/2}} dx I=∫x2−3/2(1−x)(x+1)(x2+x+1)3/2dxI = \int \frac{x^{2-3/2}(1-x)}{(x+1)(x^2+x+1)^{3/2}} dx I=∫x1/2(1−x)(x+1)(x2+x+1)3/2dxI = \int \frac{x^{1/2}(1-x)}{(x+1)(x^2+x+1)^{3/2}} dx

  2. Apply the substitution x=1tx = \frac{1}{t}: If x=1tx = \frac{1}{t}, then dx=−1t2dtdx = -\frac{1}{t^2} dt. Substitute these into the integral: I=∫(1/t)1/2(1−1/t)(1/t+1)((1/t)2+(1/t)+1)3/2(−1t2)dtI = \int \frac{(1/t)^{1/2}(1-1/t)}{(1/t+1)((1/t)^2+(1/t)+1)^{3/2}} \left(-\frac{1}{t^2}\right) dt I=∫1t(t−1t)(1+tt)(1+t+t2t2)3/2(−1t2)dtI = \int \frac{\frac{1}{\sqrt{t}}\left(\frac{t-1}{t}\right)}{\left(\frac{1+t}{t}\right)\left(\frac{1+t+t^2}{t^2}\right)^{3/2}} \left(-\frac{1}{t^2}\right) dt I=∫t−1t3/21+tt⋅(1+t+t2)3/2t3(−1t2)dtI = \int \frac{\frac{t-1}{t^{3/2}}}{\frac{1+t}{t} \cdot \frac{(1+t+t^2)^{3/2}}{t^3}} \left(-\frac{1}{t^2}\right) dt I=∫t−1t3/2⋅t1+t⋅t3(1+t+t2)3/2(−1t2)dtI = \int \frac{t-1}{t^{3/2}} \cdot \frac{t}{1+t} \cdot \frac{t^3}{(1+t+t^2)^{3/2}} \left(-\frac{1}{t^2}\right) dt I=∫(t−1)t1+3−3/2−2(1+t)(1+t+t2)3/2(−1)dtI = \int \frac{(t-1)t^{1+3-3/2-2}}{(1+t)(1+t+t^2)^{3/2}} (-1) dt I=∫(t−1)t1/2(1+t)(1+t+t2)3/2(−1)dtI = \int \frac{(t-1)t^{1/2}}{(1+t)(1+t+t^2)^{3/2}} (-1) dt I=∫(1−t)t1/2(1+t)(1+t+t2)3/2dtI = \int \frac{(1-t)t^{1/2}}{(1+t)(1+t+t^2)^{3/2}} dt

  3. Recognize a derivative for substitution: Consider the derivative of the function f(t)=1+t1+t+t2f(t) = \frac{1+t}{\sqrt{1+t+t^2}}. Using the quotient rule ddt(uv)=u′v−uv′v2\frac{d}{dt}\left(\frac{u}{v}\right) = \frac{u'v - uv'}{v^2}: u=1+t  ⟹  u′=1u = 1+t \implies u' = 1 v=1+t+t2  ⟹  v′=121+t+t2(1+2t)v = \sqrt{1+t+t^2} \implies v' = \frac{1}{2\sqrt{1+t+t^2}}(1+2t) f′(t)=1⋅1+t+t2−(1+t)1+2t21+t+t21+t+t2f'(t) = \frac{1 \cdot \sqrt{1+t+t^2} - (1+t) \frac{1+2t}{2\sqrt{1+t+t^2}}}{1+t+t^2} f′(t)=2(1+t+t2)−(1+t)(1+2t)2(1+t+t2)3/2f'(t) = \frac{2(1+t+t^2) - (1+t)(1+2t)}{2(1+t+t^2)^{3/2}} f′(t)=2+2t+2t2−(1+3t+2t2)2(1+t+t2)3/2f'(t) = \frac{2+2t+2t^2 - (1+3t+2t^2)}{2(1+t+t^2)^{3/2}} f′(t)=1−t2(1+t+t2)3/2f'(t) = \frac{1-t}{2(1+t+t^2)^{3/2}} So, 1−t(1+t+t2)3/2=2f′(t)\frac{1-t}{(1+t+t^2)^{3/2}} = 2 f'(t).

  4. Rewrite the integral using f′(t)f'(t): The integral is I=∫t1/2(1+t)⋅1−t(1+t+t2)3/2dtI = \int \frac{t^{1/2}}{(1+t)} \cdot \frac{1-t}{(1+t+t^2)^{3/2}} dt I=∫t1/21+t⋅2f′(t)dtI = \int \frac{t^{1/2}}{1+t} \cdot 2 f'(t) dt Let u=f(t)=1+t1+t+t2u = f(t) = \frac{1+t}{\sqrt{1+t+t^2}}. Then du=f′(t)dtdu = f'(t) dt. So, I=2∫t1/21+tduI = 2 \int \frac{t^{1/2}}{1+t} du.

  5. Express t1/21+t\frac{t^{1/2}}{1+t} in terms of uu: From u=1+t1+t+t2u = \frac{1+t}{\sqrt{1+t+t^2}}, we have u2=(1+t)21+t+t2u^2 = \frac{(1+t)^2}{1+t+t^2}. Consider 1−1u2=1−1+t+t2(1+t)2=(1+t)2−(1+t+t2)(1+t)21 - \frac{1}{u^2} = 1 - \frac{1+t+t^2}{(1+t)^2} = \frac{(1+t)^2 - (1+t+t^2)}{(1+t)^2} =1+2t+t2−1−t−t2(1+t)2=t(1+t)2= \frac{1+2t+t^2 - 1-t-t^2}{(1+t)^2} = \frac{t}{(1+t)^2}. Taking the square root: 1−1u2=t1+t\sqrt{1 - \frac{1}{u^2}} = \frac{\sqrt{t}}{1+t}. This simplifies to u2−1u=t1+t\frac{\sqrt{u^2-1}}{u} = \frac{\sqrt{t}}{1+t}.

  6. Substitute into the integral and evaluate: I=2∫u2−1uduI = 2 \int \frac{\sqrt{u^2-1}}{u} du. Let u=sec⁡θu = \sec \theta. Then du=sec⁡θtan⁡θdθdu = \sec \theta \tan \theta d\theta. u2−1=sec⁡2θ−1=tan⁡2θ=tan⁡θ\sqrt{u^2-1} = \sqrt{\sec^2 \theta - 1} = \sqrt{\tan^2 \theta} = \tan \theta (assuming tan⁡θ≥0\tan \theta \ge 0). I=2∫tan⁡θsec⁡θ(sec⁡θtan⁡θ)dθI = 2 \int \frac{\tan \theta}{\sec \theta} (\sec \theta \tan \theta) d\theta I=2∫tan⁡2θdθI = 2 \int \tan^2 \theta d\theta Using the identity tan⁡2θ=sec⁡2θ−1\tan^2 \theta = \sec^2 \theta - 1: I=2∫(sec⁡2θ−1)dθI = 2 \int (\sec^2 \theta - 1) d\theta I=2(tan⁡θ−θ)+CI = 2 (\tan \theta - \theta) + C.

  7. Substitute back to uu and then to xx: From u=sec⁡θu = \sec \theta, we have θ=arcsec⁡u\theta = \operatorname{arcsec} u. tan⁡θ=u2−1\tan \theta = \sqrt{u^2-1}. I=2(u2−1−arcsec⁡u)+CI = 2 (\sqrt{u^2-1} - \operatorname{arcsec} u) + C.

    Now substitute u=1+t1+t+t2u = \frac{1+t}{\sqrt{1+t+t^2}}: u2−1=t1+t+t2\sqrt{u^2-1} = \frac{\sqrt{t}}{\sqrt{1+t+t^2}}. I=2(t1+t+t2−arcsec⁡(1+t1+t+t2))+CI = 2 \left( \frac{\sqrt{t}}{\sqrt{1+t+t^2}} - \operatorname{arcsec}\left(\frac{1+t}{\sqrt{1+t+t^2}}\right) \right) + C.

    Finally, substitute t=1xt = \frac{1}{x}: t=1x\sqrt{t} = \frac{1}{\sqrt{x}}. 1+t+t2=1+1x+1x2=x2+x+1x2=x2+x+1∣x∣\sqrt{1+t+t^2} = \sqrt{1+\frac{1}{x}+\frac{1}{x^2}} = \sqrt{\frac{x^2+x+1}{x^2}} = \frac{\sqrt{x^2+x+1}}{|x|}. Since x3+x2+xx^3+x^2+x is under a square root, x>0x>0. So ∣x∣=x|x|=x. t1+t+t2=1/xx2+x+1/x=xxx2+x+1=xx2+x+1\frac{\sqrt{t}}{\sqrt{1+t+t^2}} = \frac{1/\sqrt{x}}{\sqrt{x^2+x+1}/x} = \frac{x}{\sqrt{x}\sqrt{x^2+x+1}} = \frac{\sqrt{x}}{\sqrt{x^2+x+1}}.

    1+t1+t+t2=1+1/x1+1/x+1/x2=(x+1)/xx2+x+1/x=x+1x2+x+1\frac{1+t}{\sqrt{1+t+t^2}} = \frac{1+1/x}{\sqrt{1+1/x+1/x^2}} = \frac{(x+1)/x}{\sqrt{x^2+x+1}/x} = \frac{x+1}{\sqrt{x^2+x+1}}.

    So, I=2(xx2+x+1−arcsec⁡(x+1x2+x+1))+CI = 2 \left( \frac{\sqrt{x}}{\sqrt{x^2+x+1}} - \operatorname{arcsec}\left(\frac{x+1}{\sqrt{x^2+x+1}}\right) \right) + C. Using the identity arcsec⁡(y)=arccos⁡(1/y)\operatorname{arcsec}(y) = \arccos(1/y): I=2(xx2+x+1−arccos⁡(x2+x+1x+1))+CI = 2 \left( \frac{\sqrt{x}}{\sqrt{x^2+x+1}} - \arccos\left(\frac{\sqrt{x^2+x+1}}{x+1}\right) \right) + C.

The final answer is 2(xx2+x+1−arccos⁡(x2+x+1x+1))+C\boxed{2\left(\frac{\sqrt{x}}{\sqrt{x^2+x+1}} - \arccos\left(\frac{\sqrt{x^2+x+1}}{x+1}\right)\right) + C}.

Subject: Mathematics Chapter: Integrals Topic: Integration by Substitution Difficulty: Hard Question Type: single_choice