Question
Question: Evaluate $\int \frac{(\sqrt[3]{x + \sqrt{2 - x^2}})(\sqrt[6]{1 - x\sqrt{2 - x^2}})dx}{\sqrt[3]{1 - x...
Evaluate ∫31−x2(3x+2−x2)(61−x2−x2)dx,x∈(0,1):
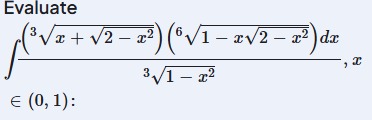
21/6x+C
Solution
To evaluate the integral ∫31−x2(3x+2−x2)(61−x2−x2)dx, for x∈(0,1), we use a trigonometric substitution.
1. Substitution: Given the term 2−x2, a suitable substitution is x=2sinθ. Then dx=2cosθdθ.
For x∈(0,1): 0<2sinθ<1⟹0<sinθ<21. This implies θ∈(0,4π).
2. Transform the terms in the integrand:
-
2−x2=2−(2sinθ)2=2−2sin2θ=2(1−sin2θ)=2cos2θ. Since θ∈(0,4π), cosθ>0, so 2cos2θ=2cosθ.
-
Numerator term 1: 3x+2−x2=32sinθ+2cosθ=32(sinθ+cosθ)=(2)1/3(sinθ+cosθ)1/3=21/6(sinθ+cosθ)1/3.
-
Numerator term 2: 61−x2−x2=61−(2sinθ)(2cosθ)=61−2sinθcosθ=61−sin(2θ). We know that 1−sin(2θ)=sin2θ+cos2θ−2sinθcosθ=(cosθ−sinθ)2. So, 61−sin(2θ)=6(cosθ−sinθ)2=(cosθ−sinθ)2/6=(cosθ−sinθ)1/3. Since θ∈(0,4π), cosθ>sinθ, so cosθ−sinθ>0.
-
Denominator term: 31−x2=31−(2sinθ)2=31−2sin2θ=3cos(2θ). Since θ∈(0,4π), 2θ∈(0,2π), so cos(2θ)>0.
3. Substitute into the integral: The product of the numerator terms is: 21/6(sinθ+cosθ)1/3⋅(cosθ−sinθ)1/3 =21/6[(sinθ+cosθ)(cosθ−sinθ)]1/3 =21/6[cos2θ−sin2θ]1/3 =21/6[cos(2θ)]1/3.
Now, substitute all terms back into the integral: I=∫[cos(2θ)]1/321/6[cos(2θ)]1/3(2cosθ)dθ I=∫21/6⋅2cosθdθ I=∫21/6⋅21/2cosθdθ I=∫21/6+3/6cosθdθ I=∫24/6cosθdθ I=∫22/3cosθdθ I=22/3sinθ+C
4. Substitute back to x: From x=2sinθ, we have sinθ=2x. I=22/3(2x)+C I=22/321/2x+C I=22/3−1/2x+C I=2(4−3)/6x+C I=21/6x+C
The final answer is 21/6x+C.
Explanation of the solution:
The integral is simplified by the substitution x=2sinθ. This transforms terms involving 2−x2 into trigonometric functions. Key identities used are 1−2sin2θ=cos(2θ) and 1−sin(2θ)=(cosθ−sinθ)2. The terms in the numerator combine to 21/6(cos(2θ))1/3, which cancels with the denominator. The integral then simplifies to 22/3∫cosθdθ=22/3sinθ+C. Substituting back sinθ=x/2 yields the final result 21/6x+C.
